

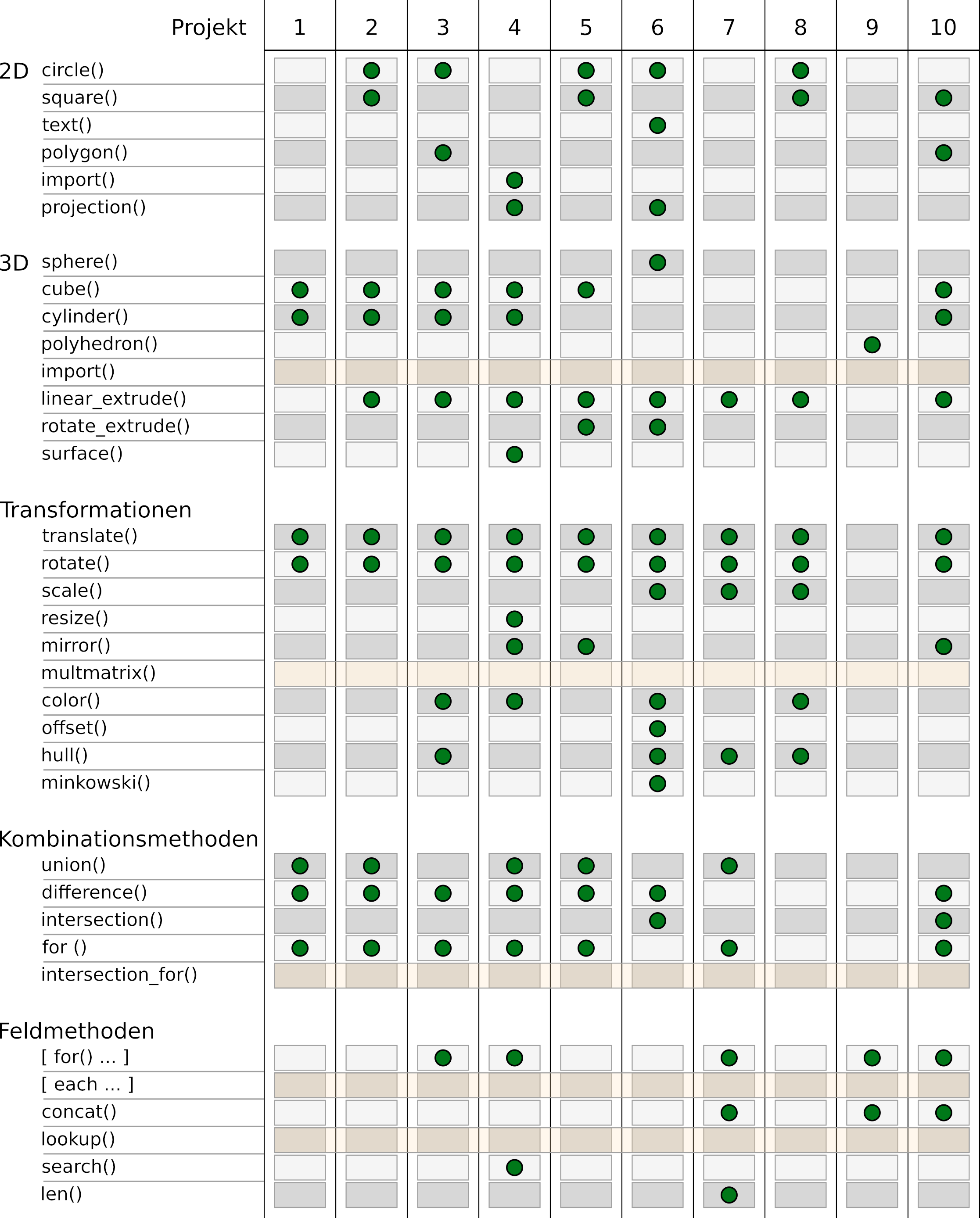
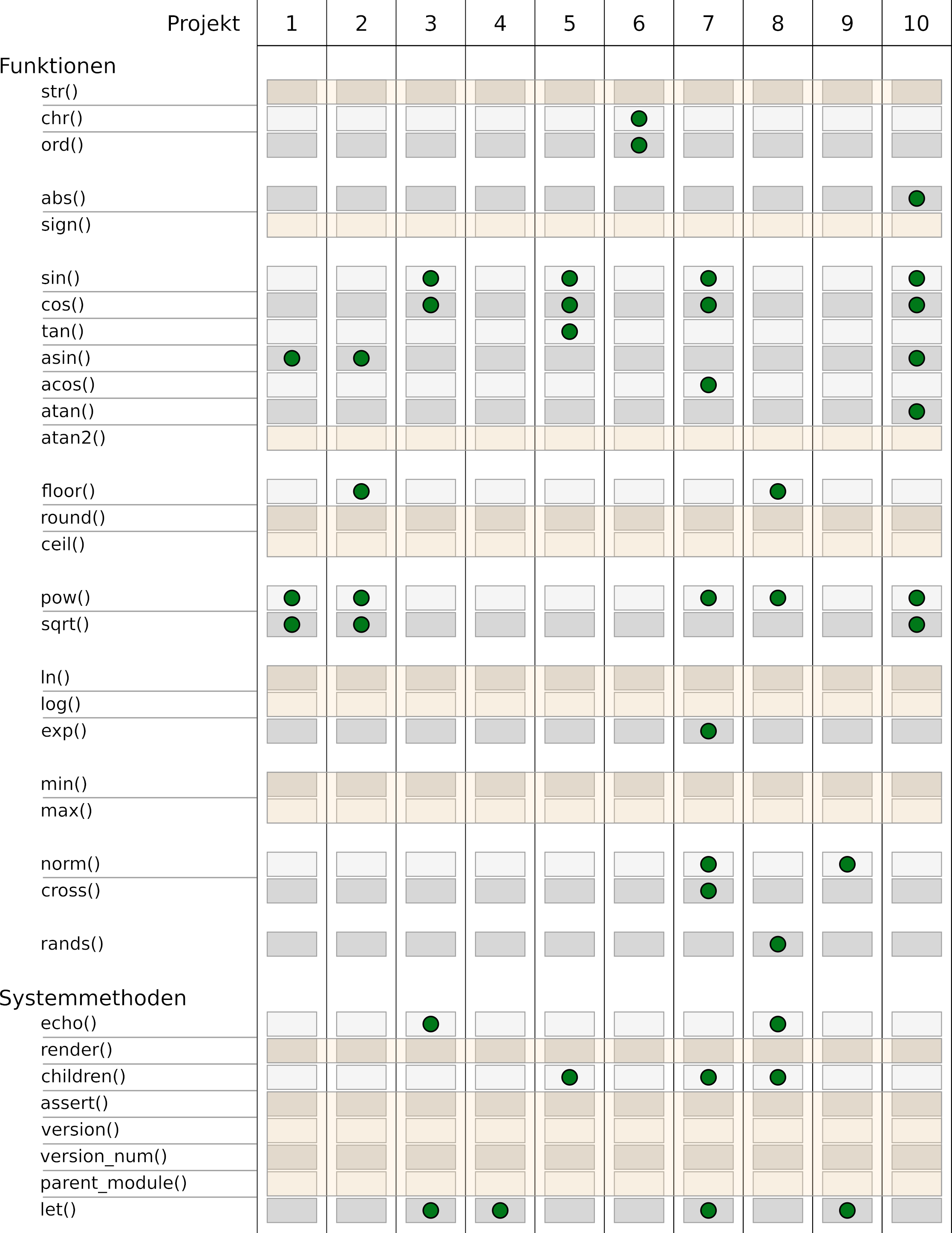
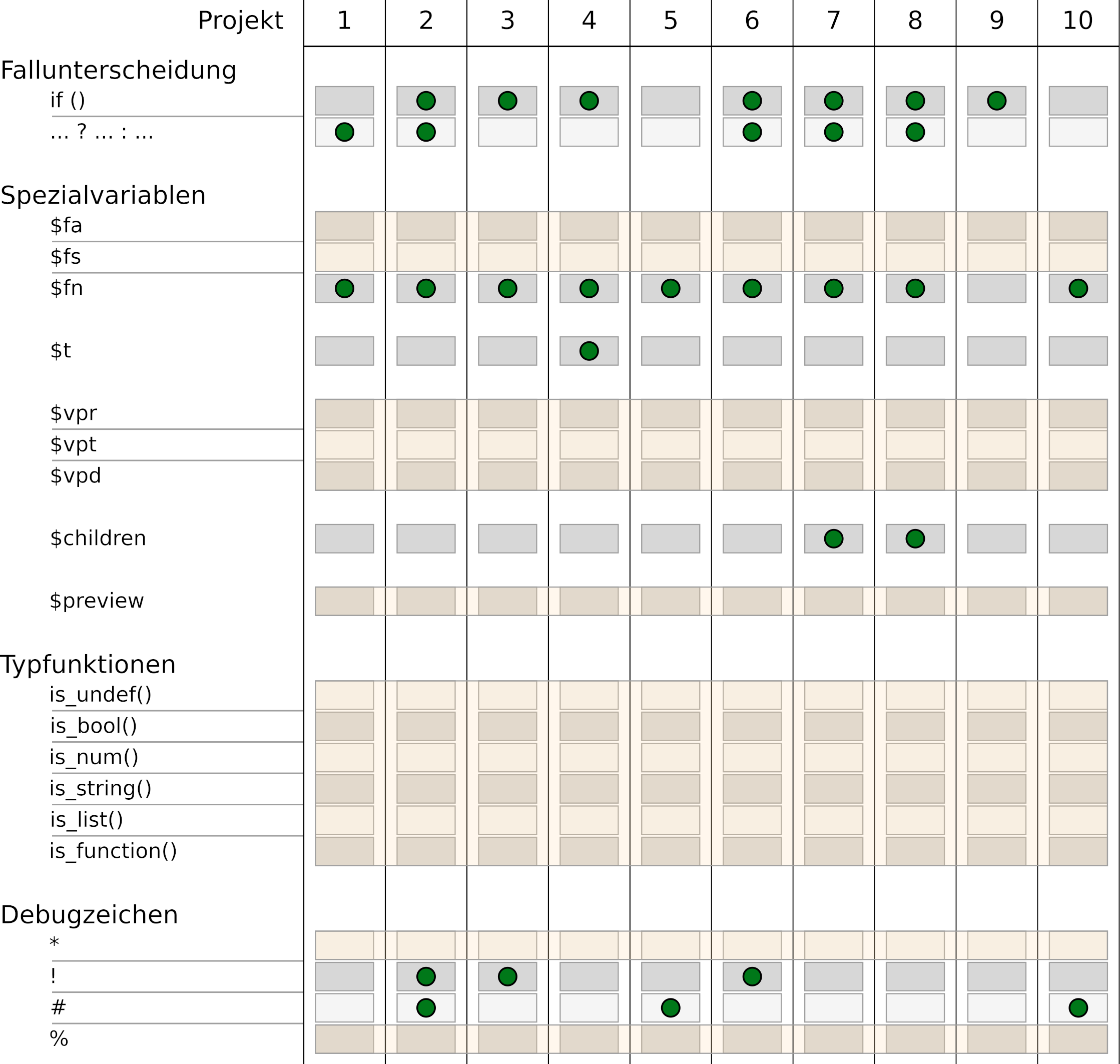
In den vergangenen 10 Projekten haben wir fast den gesamten Funktionsumfang von OpenSCAD kennengelernt. Abbildungen 13., 13.2 und 13.3 liefern hierzu eine Übersicht. Im Folgenden werden wir uns kurz und knapp mit den Funktionen beschäftigen, die wir bislang außen vor gelassen haben.
In Projekt 4 haben wir die import-Funktion genutzt, um .svg-Dateien als 2D-Grundform zu importieren. Die import-Funktion kann jedoch auch 3D-Daten in den Formaten .stl, .off, .amf und .3mf importieren. Insbesondere dann, wenn man eine komplexe und rechenintensive OpenSCAD-Geometrie in einem weiteren Projekt verwenden möchte, kann die Nutzung von import anstelle von include oder use sinnvoll sein. Auf diese Weise umgeht man in vielen Fällen eine erneute Berechnung der komplexen Geometrie. Der Nachteil ist natürlich, dass man die so importierte Geometrie nun nicht mehr direkt parametrisieren kann.
Die einzige Transformation, die wir nicht genutzt haben, ist die multmatrix-Transformation. Sie erlaubt es, eine affine Transformation der Geometrie über eine Transformationsmatrix durchzuführen. Die Matrix ist dabei eine 4 x 3 bzw. 4 x 4 Matrix deren Zellen die folgende Bedeutung haben:
M = [
// die erste Zeile kümmert sich um X
[
1, // Skalierung in X-Richtung
0, // Scherung von X entlang Y
0, // Scherung von X entlang Z
0, // Verschiebung entlang X
],
// die zweite Zeile kümmert sich um Y
[
0, // Scherung von Y entlang X
1, // Skalierung in Y-Richtung
0, // Scherung von Y entlang Z
0, // Verschiebung entlang Y
],
// die dritte Zeile kümmert sich um Z
[
0, // Scherung von Z entlang X
0, // Scherung von Z entlang Y
0, // Skalierung in Z-Richtung
0, // Verschiebung entlang Z
],
// die vierte Zeile ist immer
[0, 0, 0, 1]
];
multmatrix(M)
cube([10,10,10]);Da die vierte Zeile der Matrix M fest ist, kann sie bei Nutzung von multmatrix auch weggelassen werden. Mit der entsprechenden Belegung der Einträge der Matrix M kann man jegliche Verschiebungen und Rotationen abbilden und mittels Matrixmultiplikation zusammenfassen. In der Praxis nutzt man multmatrix eher selten. Einzig die Möglichkeit, ein Objekt in eine bestimmte Richtung zu scheren, ist manchmal von nutzen.
Wir haben in den 10 Projekten an vielen Stellen For-Schleifen genutzt. Die so entstehenden Geometrien werden dabei implizit wie bei einer Booleschen Vereinigung zusammengefasst. Dies kann man gut am folgenden Beispiel sehen:
module test() {
echo($children);
children();
}
test() {
sphere(5);
translate( [10, 0, 0] )
sphere(5);
translate( [20, 0, 0] )
sphere(5);
}
test()
for(i = [0:2])
translate( [10 * i, 10, 0] )
sphere(5);Wir definieren ein Modul test, was uns in der Konsole die Anzahl der Elemente der nachfolgenden Geometrie ausgibt. Verwenden wir test mit einer Geometriemenge ({ ... }) erhalten wir im obigen Beispiel eine Ausgabe von 3. Verwenden wir test mit einer For-Schleife, dann erhalten wir als Ausgabe eine 1. Die Geometrien, die durch die For-Schleife definiert werden, werden also zu einer einzigen Geometrie zusammengefasst. Hierdurch fehlt die Möglichkeit, eine Menge von Geometrien mittels For-Schleife zu beschreiben und dann die Boolesche Operation intersection (dt. Schnitt) auf diese Geometriemenge anzuwenden. Genau für diesen Fall gibt es deshalb die intersection_for-Schleife in OpenSCAD. In der Praxis kommt diese Art der For-Schleife nur sehr selten zum Einsatz. Sie kann aber dazu dienen, interessante Geometrien zu erzeugen. Als Beispiel mag diese diamantartige Geometrie dienen:
M = [
[1,0,1,0],
[0,1,0,0],
[0,0,1,0]
];
intersection_for(i = [0:60:359])
rotate( [0, 0, i] )
multmatrix( M )
cube( 10, center = true );Wir haben an vielen Stellen generative For-Schleifen genutzt, um Felder zu definieren. Innerhalb einer solchen generativen For-Schleife kann das Schlüsselwort each verwendet werden, um einen nachfolgenden Vektor “auszupacken”. Nehmen wir folgendes Beispiel:
vektoren = [
[1,2,3],
[4,5,6],
[7,8,9]
];
flach = [ for (v = vektoren) each v];
echo( flach );Das Feld flach ist im Ergebnis ein eindimensionales Feld, dass alle Einträge des zweidimensionalen Feldes vektoren enthält. Die Konsolenausgabe für flach ergibt daher ECHO: [1, 2, 3, 4, 5, 6, 7, 8, 9].
Die Funktion lookup erlaubt es, Werte in einem Feld von Zahlenpaaren linear zu interpolieren. Ein Beispiel:
werte = [
[-3, 2],
[ 0, 10],
[ 1, 50],
[ 4, 0]
];
echo( lookup(-1, werte) );
echo( lookup( 0, werte) );
echo( lookup( 0.5, werte) );
echo( lookup( 3, werte) );Die Konsolenausgabe hierzu sieht wie folgt aus:
ECHO: 7.33333
ECHO: 10
ECHO: 30
ECHO: 16.6667Die Funktion lookup durchsucht das ihr übergebene Feld von Zahlenpaaren nach den zwei benachbarten Zahlenpaaren, deren jeweils erste Werte ein Intervall aufspannen, in dem der übergebene Suchparameter liegt. Anschließend werden die zweiten Werte dieser beiden Paare gewichtet gemittelt, so dass die Mittlung der Nähe des Suchparameters zu den jeweiligen ersten Werten entspricht.
Wir haben in unseren Projekten einen großen Teil der von OpenSCAD bereitgestellten Funktionen genutzt. Nicht genutzt haben wir die Funktionen str, sign, atan2, round, ceil, ln, log, min und max.
Die Funktion str erzeugt aus ihren Parametern eine einzelne, zusammenhängende Zeichenkette. Sie erinnern sich an die Variable srnd aus Projekt 8? Wir nutzten die Variable für die Initialisierung der Zufallszahlen und gaben mittels echo( srnd ); ihren Wert in der Konsole aus, um sie uns für eine spätere, manuelle Verwendung merken zu können. Wir hätten diese Konsolenausgabe mit der str-Funktion etwas lesbarer gestalten können, z.B. echo( str("Als Initialisierungswert wurde ", srnd, " genutzt.") );.
Die Funktion sign liefert das Vorzeichen einer Zahl zurück. Bei negativen Zahlen liefert sign eine -1, bei positiven Zahlen eine 1 und bei null eine 0 zurück.
Die Funktion atan2 ist eine Variante des Arkustangens. Der “normale” Arkustangens kann zwischen y/x und -y/-x nicht unterscheiden, da sich die Minuszeichen im zweiten Fall aufheben würden. Die Funktion atan2 löst dieses Problem, indem man y und x als getrennte Parameter an die Funktion übergeben kann.
Die Funktion round rundet den übergebenen Kommawert kaufmännisch. Die Funktion ceil rundet den übergebenen Wert immer auf.
Die Funktion ln liefert den natürlichen Logarithmus der übergebenen Zahl. Die Funktion log liefert den Logarithmus zur Basis 10.
Die Funktion min liefert als Ergebnis den kleinsten Wert der ihr übergebenen Parameter zurück. Besteht der Parameter aus nur einem einzigen Vektor, wir das kleinste Element innerhalb des Vektors zurückgegeben. Die Funktion max verhält sich analog. Sie liefert das jeweils größte Element zurück.
In seltenen Fällen kann es passieren, dass die Vorschau (F5) einer Geometrie fehlschlägt und es zu Artefakten kommt, denen man nicht mit anderen Mitteln (z.B. einem convexity Parameter) beikommen kann. Mit der Funktion render, die man jeder Geometrie wie eine Transformation voranstellen kann (z.B. render() sphere( 10 );), kann man OpenSCAD dazu zwingen, den entsprechenden Teil der Geometrie auch schon während einer Vorschau vollständig zu berechnen.
Ein anderer Einsatzzweck von render besteht darin, komplexe Geometrien bereits in der Vorschau in ein 3D-Gittermodell zu überführen und damit die Vorschau flüssiger zu machen. Dies kann insbesondere bei aufwendigen Booleschen Operationen hilfreich sein.
Die Funktion assert erlaubt die Prüfung von Annahmen und ermöglicht die Ausgabe einer entsprechenden Fehlermeldung, wenn diese Annahmen nicht erfüllt sind. Dies ist insbesondere dann nützlich, wenn wir Module entwickeln, die von Anderen als Library genutzt werden sollen. Nehmen wir mal an, wir erwarten einen dreidimensionalen Vektor als Eingabe. Dann könnte eine Prüfung wie folgt aussehen:
module mein_modul( groesse ) {
assert(
len(groesse) == 3,
"Parameter groesse muss ein dreidimensionaler Vektor sein!"
);
}Würden wir nun das Modul z.B. mit einer einfachen Zahl aufrufen, dann würden wir eine Fehlermeldung in der Konsole erhalten:
ERROR: Assertion '(len(groesse) == 3)' failed: "Parameter groesse muss ein dreidimensionaler Vektor sein!"Die weiter unten beschriebenen Typfunktionen können in diesem Zusammenhang sehr nützlich sein.
Die Funktionen version und version_num liefern die aktuelle Version von OpenSCAD zurück. Die Funktion version liefert einen dreidimensionalen Vektor mit den einzelnen Versionsbestandteilen. Die Funktion version_num liefert eine einzelne Zahl, die die jeweilige Version eindeutig repräsentiert.
Eine derartige Versionsabfrage ist dann von Nutzen, wenn wir eine Geometriebibliothek entwickeln und Funktionen verwenden, die in früheren OpenSCAD-Versionen nicht vorhanden sind oder anders parametrisiert wurden. Durch entsprechende Fallunterscheidungen kann man es dann ggf. erreichen, dass die Bibliothek stabil über mehrere Versionen von OpenSCAD hinweg funktioniert.
Die Funktion parent_module liefert den Namen eines übergeordneten Moduls innerhalb einer Modulhierarchie, wenn alle Module innerhalb der Hierarchie mittels children auf nachgeordnete Elemente zugreifen. Das offizielle Handbuch von OpenSCAD gibt als Anwendungsbeispiel die Erzeugung einer Materialliste für eine gegebene Geometrie an. In der Praxis spielt diese Funktion keine Rolle.
In unseren Projekten haben wir häufig die Spezialvariable $fn genutzt, um die Feinheit runder Geometrien einzustellen. Auf ähnliche Weise kann man die Feinheit runder Geometrien auch mittels der Variablen $fa und $fs steuern. Mit $fa kann man die minimalen Winkel einer Geometrie festlegen und mit $fs die minimale Größe der Teilflächen. In beiden Fällen erzeugen kleinere Werte eine feinere Geometrie. Standardmäßig steht $fa auf 12 und $fs auf 2.
Die Spezialvariablen $vpr, $vpt und $vpd liefern Informationen über die aktuelle Perspektive im Vorschaufenster wenn eine neue Vorschau berechnet wird. $vpr liefert die Rotation, $vpt die Verschiebung und $vpd die Distanz der Kamera.
Durch das Setzen dieser Variablen kann man die Perspektive im Anzeigefenster ändern. Dies könnte man zum Beispiel für die Erzeugung von Kamerafahrten im Zusammenhang mit den Animationsfähigkeiten von OpenSCAD nutzen.
Die Spezialvariable $preview liefert true, wenn eine Vorschau (F5) berechnet wird und false, wenn eine vollständige Geometrieberechnung (F6) ausgeführt wird.
OpenSCAD stellt eine Reihe von Funktionen zur Verfügung, mit denen der Typ einer Variable geprüft werden kann. Diese Prüfung ist insbesondere im Zusammenhang mit der assert-Funktion von nutzen, oder für den Fall, dass man einen Parameter mit einer doppelten Funktionalität ausstatten möchte. Ein existierendes Beispiel hierfür ist der scale-Parameter der linear_extrude-Transformation. Der Parameter kann entweder eine Zahl oder ein Vektor sein. Ist er eine Zahl, wird die zugrunde liegende 2D-Form in alle Richtungen gleichmäßig skaliert. Ist der Parameter ein Vektor, kann für die X- und Y-Richtung eine jeweils individuelle Skalierung angegeben werden.
Die zur Verfügung stehenden Typfunktionen sind: is_undef, is_bool, is_num, is_string, is_list und (in zukünftigen OpenSCAD-Versionen) is_function. Mit list sind hier jegliche Art von Feldern bzw. Vektoren gemeint.
Neben den bekannten Debugzeichen ! und # gibt es auch noch das *-Zeichen und das %-Zeichen. Mit dem *-Zeichen kann man einen Geometrieteil “abschalten”. Es stellt also eine Alternative zum auskommentieren dar. Mit dem %-Zeichen kann man einen Geometrieteil transparent schalten.
Mit dieser abschließenden Kurzzusammenfassung kennen Sie nun alle OpenSCAD-Funktionen!