

In diesem Projekt wollen wir einen Stiftehalter konstruieren, der viel Platz für unsere Schreibtischutensilien bereit hält und trotz überhängender Elemente ohne Stützstruktur 3D-gedruckt werden kann. Hierzu lassen wir uns von der gotischen Baukunst inspirieren.

Wir lernen die Rotationsextrusion rotate_extrude kennen und verfolgen diesmal einen explorativen Designansatz, der das finale Modul “von innen heraus” entwickelt.
Kernelement des Stiftehalters sind die gotisch anmutenden Bögen an der Außenseite. Um diese Bögen zu erstellen, bietet sich die Rotationsextrusion rotate_extrude an. Ähnlich wie die lineare Extrusion linear_extrude wirkt rotate_extrude auf eine nachfolgende 2D-Geometrie und erzeugt aus dieser ein 3D-Objekt. Im Gegensatz zu linear_extrude wird die 2D-Geometrie jedoch nicht entlang einer Gerade sondern entlang einer (impliziten) Kurve extrudiert.
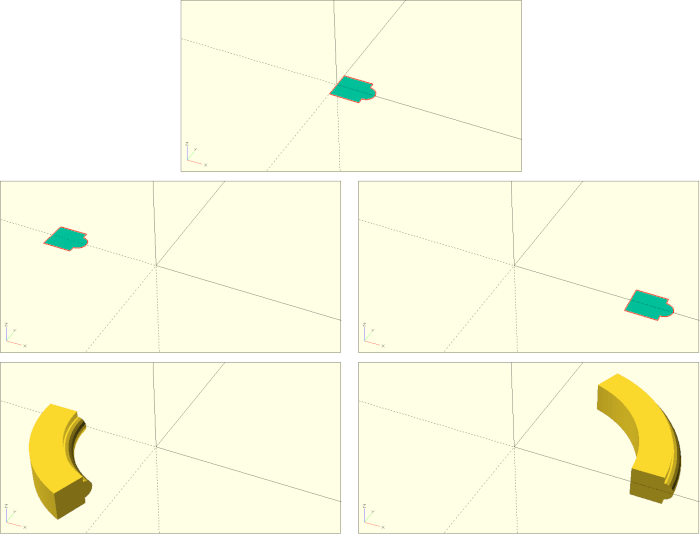
Die Transformation rotate_extrude ist insofern etwas gewöhnungsbedürftig, da einige ihrer Eigenschaften implizit durch die Position der 2D-Geometrie, die extrudiert wird, gegeben ist. Man kann sich die Funktionsweise von rotate_extrude in etwa so vorstellen: die gegebene 2D-Geometrie wird um die X-Achse in die Senkrechte gedreht. Anschließend wird die Geometrie um die Z-Achse im Uhrzeigersinn gedreht und dabei extrudiert. Das Ergebnis hängt also sehr davon ab, wo sich die 2D-Geometrie zuvor befunden hat (Abbildung 7.).
Beginnen wir unseren Bogen mit einer 2D-Geometrie, die aus einem Quadrat und einem Kreis besteht und testen wir, ob wir ein entsprechendes Bogenstück erzeugt bekommen:
bogen_grundseite = 5;
bogen_winkel = 70;
bogen_radius = 20;
rotate( [-90, 0, 0])
rotate_extrude( angle = bogen_winkel, $fn = 100 )
translate( [-bogen_radius, 0] )
union(){
translate( [0, -bogen_grundseite / 2] )
square( bogen_grundseite );
translate( [bogen_grundseite, 0] )
circle( d = bogen_grundseite * 3 / 5, $fn = 18);
}Wir erzeugen ein Quadrat (square) mit Seitenlänge bogen_grundseite und verschieben es mittig auf die X-Achse. Da wir uns im zweidimensionalen befinden, benötigt unsere Verschiebetransformation translate auch nur einen zweidimensionalen Vektor als Eingabe. Zusätzlich definieren wir noch einen Kreis (circle), der im Durchmesser 3/5 der Kantenlänge des Quadrats hat und positionieren den Kreis an die Außenkante des Quadrats. Wir verbinden Quadrat und Kreis zu einer gemeinsamen 2D-Geometrie mittels der Booleschen Vereinigung (union).
An dieser Stelle können wir nun den Radius unseres Bogens bestimmen, indem wir die 2D-Geometrie entlang der X-Achse vom Ursprung wegbewegen. Da wir den Kreis unserer Geometrie auf der Innenseite des Bogens haben wollen, schieben wir unsere Geometrie in negativer X-Richtung (translate( [-bogen_radius, 0] )). Erst jetzt wenden wir die rotate_extrude-Transformation an, um unser Bogenstück zu erzeugen. Der Parameter angle gibt hierbei an, wie weit die 2D-Geometrie gedreht werden soll. Ein Winkel von 360 würde einen Ring ergeben. In älteren Versionen von OpenSCAD konnte kein Winkel angegeben werden und es wurde immer ein vollständiger Ring erzeugt. Im Anschluß an die Rotationsextrusion liegt unser Bogenstück noch auf der Seite. Mit einer Rotation um die X-Achse können wir schließlich den Bogen aufrichten.
Wir können nun die gegenüberliegende Seite des Bogens auf einfache Weise mit einer Kombination von For-Schleife und Spiegeltransformation (mirror) erzeugen:
bogen_grundseite = 5;
bogen_winkel = 70;
bogen_radius = 20;
for (m = [0:1])
mirror( [m, 0, 0] )
rotate( [-90, 0, 0])
rotate_extrude( angle = bogen_winkel, $fn = 100 )
translate( [-bogen_radius, 0] )
union(){
translate( [0, -bogen_grundseite / 2] )
square( bogen_grundseite );
translate( [bogen_grundseite, 0] )
circle( d = bogen_grundseite * 3 / 5, $fn = 18);
}Die Schleifenvariable m nimmt genau einmal den Wert 0 und einmal den Wert 1 an und erzeugt damit eine normale und eine gespiegelte Version unseres Bogenstücks. Nun klafft jedoch eine Lücke zwischen unseren Bögen, die wir noch schließen müssen. Das Problem ist, dass unser ursprüngliches Bogenstück mit seiner Oberkante am Ende des Bogens nicht direkt die Z-Achse berührt. Dadurch entsteht beim Spiegeln eine Lücke. Wir müssen also unser Bogenstück vor dem Spiegeln passend an die Z-Achse heranschieben:
bogen_grundseite = 5;
bogen_winkel = 70;
bogen_radius = 20;
for (m = [0:1])
mirror( [m, 0, 0] )
translate( [cos(bogen_winkel) * bogen_radius, 0, 0] )
rotate( [-90, 0, 0])
rotate_extrude( angle = bogen_winkel, $fn = 100 )
translate( [-bogen_radius, 0] )
union(){
translate( [0, -bogen_grundseite / 2] )
square( bogen_grundseite );
translate( [bogen_grundseite, 0] )
circle( d = bogen_grundseite * 3 / 5, $fn = 18);
}Es zeigt sich, dass der Abstand zur Z-Achse durch cos(bogen_winkel) * bogen_radius beschrieben werden kann. Dies ist erstmal nicht offensichtlich. Es hilft, sich die Situation einmal zu skizzieren, das “passende” rechtwinklige Dreieck zu identifizieren und dann bei Wikipedia nachzuschlagen, wie das denn nochmal mit dem Cosinus war… (cos(a) = Ankathete / Hypothenuse).
Wenn wir jetzt ein wenig mit den Parametern bogen_radius und bogen_winkel spielen, dann sehen wir, dass die beiden Bogenhälften immer sauber aneinanderliegen. Für die weitere Verwendung unseres Bogens ist die bisherige Parametrisierung ein wenig unkomfortabel. Idealerweise würden wir lieber die Breite des kompletten Bogens von Außenkante zu Außenkante festlegen und den Radius passend dazu berechnen. Dies geht auf folgende Weise:
bogen_breite = 50;
bogen_grundseite = 5;
bogen_winkel = 70;
bogen_radius = bogen_breite / (2 - 2 * cos(bogen_winkel) );
for (m = [0:1])
mirror( [m, 0, 0] )
translate( [cos(bogen_winkel) * bogen_radius, 0, 0] )
rotate( [-90, 0, 0])
rotate_extrude( angle = bogen_winkel, $fn = 100 )
translate( [-bogen_radius, 0] )
union(){
translate( [0, -bogen_grundseite / 2] )
square( bogen_grundseite );
translate( [bogen_grundseite, 0] )
circle( d = bogen_grundseite * 3 / 5, $fn = 18);
}Auch in diesem Fall ist es hilfreich, sich die ganze Sache zu skizzieren und eine Gleichung aufzustellen, die einen Bezug zwischen bogen_winkel, bogen_radius und bogen_breite herstellt. Diese Gleichung kann man dann so umformen, dass bogen_radius nur noch alleine auf einer Seite des Gleichheitszeichens steht.
Was uns jetzt noch fehlt sind zwei senkrechte Säulen unterhalb unseres Bogens. Diese können wir mit der gleichen Grundform und einer linearen Extrusion beschreiben. Jetzt ist auch ein guter Zeitpunkt, das ganze schonmal in ein Modul zu verpacken:
module bogen(
bogen_breite,
bogen_grundseite,
bogen_winkel,
saeulen_hoehe
) {
bogen_radius = bogen_breite / (2 - 2 * cos(bogen_winkel) );
module grundform() {
union(){
translate( [0, -bogen_grundseite / 2] )
square( bogen_grundseite );
translate( [bogen_grundseite, 0] )
circle( d = bogen_grundseite * 3 / 5, $fn = 18);
}
}
translate( [0, 0, saeulen_hoehe] )
for (m = [0:1])
mirror( [m, 0, 0] )
translate( [cos(bogen_winkel) * bogen_radius, 0, 0] )
union(){
rotate( [-90, 0, 0])
rotate_extrude( angle = bogen_winkel, $fn = 100 )
translate( [-bogen_radius, 0] )
grundform();
translate( [0, 0, -saeulen_hoehe] )
linear_extrude( height = saeulen_hoehe )
translate( [-bogen_radius, 0] )
grundform();
}
}
bogen(
bogen_breite = 50,
bogen_grundseite = 5,
bogen_winkel = 75,
saeulen_hoehe = 50
);Wir haben aus den Variablen bogen_breite, bogen_grundseite und bogen_winkel Parameter des neuen Moduls bogen gemacht. Neu hinzugekommen ist der Parameter saeulen_hoehe. Innerhalb des Moduls haben wir unsere 2D-Grundform in ein Untermodul gekapselt, da wir die Grundform an zwei Stellen brauchen - für den Bogen und für die Säulen. An der Stelle, wo wir unser ursprüngliches Bogenstück mittels Drehung um die X-Achse aufgerichtet haben, haben wir die Geometriebeschreibung des Bogens aufgetrennt und eine Boolesche Vereinigung (union) eingefügt. Auf diese Weise können wir unterhalb des Bogenstücks eine Säule anfügen, die dann im weiteren Verlauf mitverschoben und gespiegelt wird.
Es gibt noch einen Schönheitsfehler in unserer Geometriebeschreibung. Wenn wir kleine Winkel nutzen, z.B. 30 Grad, dann “durchbrechen” sich die Spitzen der gespiegelten Bogenteile. Um dies zu verhindern, müssen wir die Spitzen noch sauber abschneiden. Dies können wir mit einer Booleschen Differenzoperation erreichen, die wir direkt vor der Spiegel-Transformation platzieren:
/* ... */
translate( [0, 0, saeulen_hoehe] )
for (m = [0:1])
mirror( [m, 0, 0] )
difference(){
translate( [cos(bogen_winkel) * bogen_radius, 0, 0] )
union(){
rotate( [-90, 0, 0])
rotate_extrude( angle = bogen_winkel, $fn = 100 )
translate( [-bogen_radius, 0] )
grundform();
translate( [0, 0, -saeulen_hoehe] )
linear_extrude( height = saeulen_hoehe )
translate( [-bogen_radius, 0] )
grundform();
}
translate([
0,
-bogen_grundseite,
sin(bogen_winkel) * bogen_radius - 5 * bogen_grundseite
])
cube( 5 * bogen_grundseite);
}
/* ... */Nun können wir unser Modul bogen benutzen, um aus ihm das Seitenteil unseres Stiftehalters zu definieren. Hierzu instanziieren wir das Modul mehrfach mit jeweils angepassten Parametern und verschieben die einzelnen Teile auf geeignete Weise zueinander:
bogen_breite = 60;
bogen_grundseite = 5;
bogen_winkel = 50;
saeulen_hoehe = 75;
// Hauptbogen
bogen(
bogen_breite,
bogen_grundseite,
bogen_winkel,
saeulen_hoehe
);
faktor_breite = 2 / 3;
faktor_grundseite = 3 / 5;
// Innere Hauptbögen
verschiebung_x1 =
(bogen_breite -
bogen_breite * faktor_breite -
bogen_grundseite / 2) / 2;
for(v = [-1:2:1])
translate( [verschiebung_x1*v, 0, 0] )
bogen(
bogen_breite * faktor_breite,
bogen_grundseite * faktor_grundseite,
bogen_winkel * 0.82,
saeulen_hoehe
);
// Innere Seitenbögen
verschiebung_x2 =
(bogen_breite -
bogen_breite * (1 - faktor_breite) -
bogen_grundseite / 2) / 2;
for(v = [-1:2:1])
translate( [verschiebung_x2*v, 0, 0] )
bogen(
bogen_breite * (1 - faktor_breite),
bogen_grundseite * faktor_grundseite,
bogen_winkel * 0.58,
saeulen_hoehe
);Die resultierende Geometriebeschreibung ist im Grunde nicht sonderlich kompliziert, jedoch ein wenig unübersichtlich. Ist man mit einer solchen Beschreibung konfrontiert und möchte sich eine Übersicht darüber verschaffen, welcher Teil der Geometriebeschreibung welcher Komponente im Ausgabefenster entspricht, ist die Hervorhebung einzelner Teile mittels vorangestelltem #-Zeichen sehr hilfreich. Wie schon bei der Beschreibung eines einzelnen Bogens benutzen wir auch hier eine For-Schleife, um jeweils eine Geometriekopie zu definieren. In diesem Fall wird die nachfolgende Geometriebeschreibung nicht gespiegelt, sondern einmal negativ und einmal positiv entlang der X-Achse verschoben. Dies wird erreicht, indem die Schleifenvariable einmal den Wert -1 und einmal den Wert 1 annimmt. Damit die Schleifenvariable auf dem Weg von -1 nach 1 nicht auch den Wert 0 annimmt, ist die Schrittweite auf 2 gesetzt.
Nun können wir auch das Seitenteil in ein Modul auslagern und das Modul bogen zum Untermodul dieses Moduls werden lassen:
module seitenteil(
bogen_breite,
bogen_grundseite,
bogen_winkel,
saeulen_hoehe
) {
module bogen(
bogen_breite,
bogen_grundseite,
bogen_winkel,
saeulen_hoehe
) {
/* ... */
}
// Hauptbogen
/* ... */
// Innere Hauptbögen
/* ... */
// Innere Seitenbögen
/* ... */
}
bogen_breite = 60;
bogen_grundseite = 5;
bogen_winkel = 50;
saeulen_hoehe = 75;
seitenteil(
bogen_breite,
bogen_grundseite,
bogen_winkel,
saeulen_hoehe
);Obwohl das Modul seitenteil und sein Untermodul bogen nun gleichnamige Parameter besitzen, kommt es nicht zu Verwechselungen (zumindest nicht auf Seiten von OpenSCAD). Die jeweils “inneren” Variablen überdecken die “äußeren”. Im Modul bogen ist also der Parameter bogen_breite des Moduls seitenteil nicht mehr sichtbar. Es kann nur noch auf den Parameter bogen_breite des Moduls bogen zugegriffen werden.
Nun können wir das Modul seitenteil nutzen, um unseren Stiftehalter zu beschreiben. Beginnen wir mit einer hexagonalen Anordnung der Seitenteile:
bogen_breite = 60;
bogen_grundseite = 5;
bogen_winkel = 50;
saeulen_hoehe = 75;
hexagonal_height = bogen_breite / ( 2 * tan(30) );
for (r = [0:60:359])
rotate( [0, 0, r] )
translate( [0, hexagonal_height - bogen_grundseite / 2, 0] )
seitenteil(
bogen_breite,
bogen_grundseite,
bogen_winkel,
saeulen_hoehe
);Um ein Hexagon zu erzeugen, müssen wir ein Seitenteil passend entlang der Y-Achse verschieben und es dann 5 mal um 60 Grad um die Z-Achse drehen. Für die Verschiebung entlang der Y-Achse müssen wir den Abstand der Seitenkanten zum Zentrum des Hexagons ausrechnen. Auch hier hilft es, sich das ganze einmal aufzuzeichnen. Die senkrechte Linie vom Zentrum des Hexagons auf die Mitte eines Seitenteils hat zum Radius des Hexagons einen Winkel von 30 Grad. Der Radius ist in dem entstehenden Dreieck die Hypothenuse. Die Mittelsenkrechte ist die Ankathete und die Hälfte des Seitenteils ist die Gegenkathete. Da der Tangens des Winkels gleich Ankathete durch Gegenkathete ist (und wir an der Ankathete interessiert sind), liefert Gegenkathete / tan(30) die gesuchte Länge der Mittelsenkrechten. Da die Gegenkathete die Hälfte des Seitenteils mit Länge bogen_breite ist, landen wir schließlich bei (bogen_breite / 2) / tan(30), was man wiederum auch als bogen_breite / (2 * tan(30) ) schreiben kann.
Da wir die Seitenteile mittig auf der X-Achse stehend konstruiert haben, müssen wir sie um bogen_grundseite / 2 weniger verschieben als gerade ausgerechnet. Als nächstes beschreiben wir den Boden des Stiftehalters und einen Seitenrand:
bogen_breite = 60;
bogen_grundseite = 5;
bogen_winkel = 50;
saeulen_hoehe = 75;
boden_dicke = 1;
rand_hoehe = 5;
rand_dicke = 3;
hexagonal_height = bogen_breite / ( 2 * tan(30) );
for (r = [0:60:359])
rotate( [0, 0, r] )
translate( [0, hexagonal_height - bogen_grundseite / 2, 0] )
union() {
seitenteil(
bogen_breite,
bogen_grundseite,
bogen_winkel,
saeulen_hoehe
);
// bodenplatte
translate( [-bogen_breite / 2, -hexagonal_height, 0] )
cube( [bogen_breite, hexagonal_height, boden_dicke] );
// rand
translate( [-bogen_breite / 2, -rand_dicke / 2, 0] )
cube( [bogen_breite, rand_dicke, rand_hoehe] );
}Wir nutzen an dieser Stelle einfach die Symmetrie des Hexagons aus und beschreiben jeweils nur einen Teil der Bodenplatte und einen Teil des Randes und nutzen eine Boolesche Vereinigung (union), um diese Teile zusammen mit dem Seitenteil auszurichten und zu drehen.
Zum Schluss kümmern wir uns noch um das Innenleben des Stiftehalters. Dies besteht aus einem hohlen Zylinder und sechs Innenwänden:
/* ... */
zylinder_dm = 50;
zylinder_hoehe = 100;
zylinder_wandung = 2;
hexagonal_height = bogen_breite / ( 2 * tan(30) );
hexagonal_radius = bogen_breite / ( 2 * sin(30) );
/* ... */
// Zylinder in der Mitte
difference() {
cylinder( d = zylinder_dm, h = zylinder_hoehe ,$fn = 50);
translate( [0, 0, boden_dicke] )
cylinder(
d = zylinder_dm - 2 * zylinder_wandung,
h = zylinder_hoehe ,
$fn = 50
);
}
// Innenwände
for (r = [0:60:359])
rotate( [0, 0, r] )
translate( [zylinder_dm/2 - 0.1, -zylinder_wandung / 2, 0] )
cube([
hexagonal_radius - zylinder_dm/2 - bogen_grundseite / 2,
zylinder_wandung,
saeulen_hoehe
]);Wir erzeugen den hohlen Zylinder in der Mitte mittels einer Booleschen Differenzoperation, bei der wir einfach einen zweiten, kleineren und nach oben verschobenen Zylinder abziehen. Für die Innenwände benötigen wir nun den Radius des Hexagons. Man kann den Radius mit den gleichen Überlegungen wie zuvor herleiten. Nur dass man hier nicht den Tangens sondern den Sinus verwendet. Die Innenwände bestehen aus einem Rechteck, das zunächst passend verschoben und dann fünf mal um 60 Grad gedreht und dabei kopiert wird.
Die Überhänge in unserem Stiftehalter sind so gering gehalten, dass man den Halter ohne Stützstruktur drucken können sollte. Der Druck wird desto anspruchsvoller, je größer wir bogen_winkel wählen. Sollten Sie Probleme mit dem Drucken der Überhänge haben, versuchen Sie die Schichthöhe (engl. layer height) in ihrem Slicer-Programm zu verringern. Alternativ können Sie auch versuchen, die Linienbreite (engl. line width) zu vergrößern. Mit einer typischen 0.4 Millimeter Düse sollten sie ohne weiteres Linienbreiten von 0.5 bis 0.6 Millimetern drucken können. Zu guter Letzt kann man auch versuchen, die Druckgeschwindigkeit zu reduzieren. Dann hat das Gebläse an der Druckdüse mehr Zeit, das frisch gedruckte Plastik herunterzukühlen.