

In diesem Projekt wollen wir ein parametrisierbares Lüfterrad konstruieren, bei dem insbesondere der Anstellwinkel und die Verdrehung der Blätter einstellbar sind.
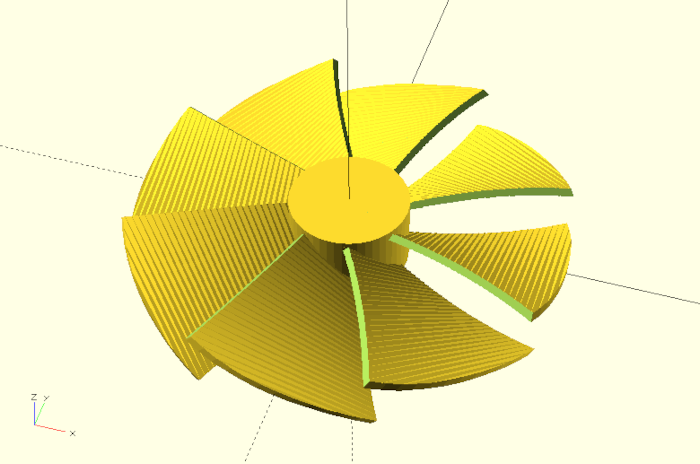
Wir werden eine neue Seite der linear_extrude-Transformation kennenlernen und die mathematischen Funktionen abs und atan nutzen.
Beginnen wir mit der Definition eines Hauptmoduls luefterrad, einer Reihe von Parametern und einem Untermodul blatt, in dem wir die Geometrie eines einzelnen Blattes des Lüfterrads beschreiben werden:
module luefterrad(
blaetter = 8,
aussenradius = 55,
innenradius = 15,
aussenbreite = 50,
innenbreite = 20,
materialstaerke = 2,
twist = -30,
anstellwinkel = 45,
){
module blatt() {
}
blatt(); // debug
}
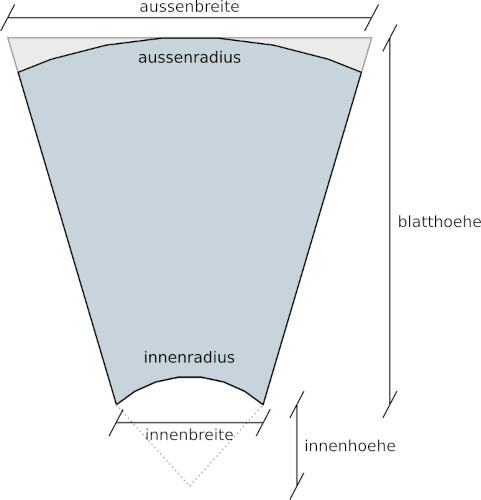
luefterrad();Bis auf den Parameter blaetter, der die Anzahl der Lüfterblätter bestimmt, beziehen sich alle anderen Parameter auf geometrische Eigenschaften eines einzelnen Lüfterblattes. Abbildung 12. zeigt schematisch, welche Eigenschaften eines Blattes die Parameter aussenradius, innenradius, aussenbreite und innenbreite bestimmen. Die Werte innenhoehe und blatthoehe in Abbildung 12. werden wir später berechnen. Die Parameter twist und anstellwinkel beeinflussen die Verwindung des Lüfterblatts sowie den Winkel des Blatts an der Lüfternabe. Der Parameter materialstaerke bestimmt die Dicke des Lüfterblatts.
Innerhalb des Moduls luefterrad haben wir das Untermodul blatt sowie eine Testinstanz dieses Moduls angelegt. Lassen Sie uns mit der Geometriebeschreibung eines einzelnen Blattes anfangen:
module luefterrad(
/* ... */
){
module blatt() {
innenhoehe =
cos(
asin( innenbreite / ( 2 * innenradius ) )
) * innenradius;
blatthoehe = aussenradius - innenhoehe;
translate( [0, innenhoehe, 0] )
rotate( [-90, 0, 0] )
linear_extrude(
height = blatthoehe,
twist = twist,
slices = 10 ,
convexity = 10
)
square( [aussenbreite, materialstaerke], center = true );
}
blatt(); // debug
}
/* ... */Wir berechnen zunächst die Werte innenhoehe und blatthoehe (Abbildung 12.). Die innenhoehe ist der Punkt, wo sich die Senkrechte mit Abstand innebreite / 2 vom Ursprung und der Kreis mit innenradius treffen. Um die innenhoehe auszurechnen brauchen wir den Winkel zwischen Radius und Senkrechte in diesem Schnittpunkt (asin( innenbreite / ( 2 * innenradius ) )). Anschließend können wir die innenhoehe mit Hilfe des Cosinus und des innenradius bestimmen. Die blatthoehe ist der Rest der Distanz von innenhoehe zum aussenradius.
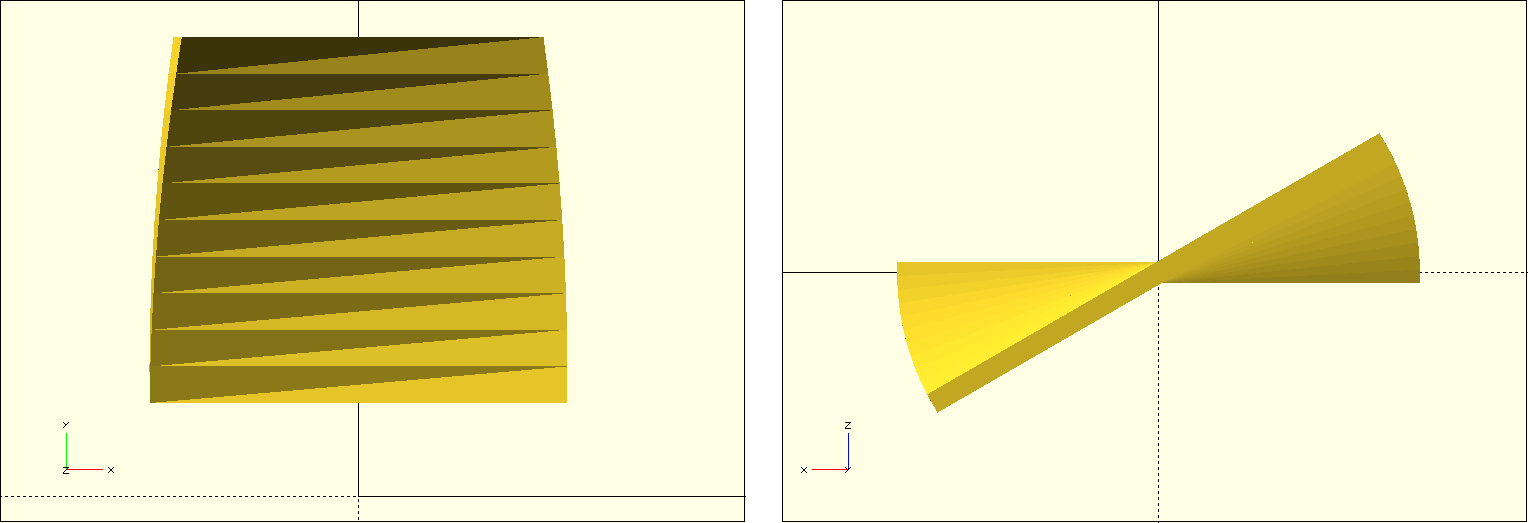
Das Blatt selbst modellieren wir mittels der 2D-Grundform square und der linearen Extrusion. Neu ist, dass wir nun den Parameter twist benutzen, um die Grundform während der Extrusion zu drehen (Abbildung 12.). Mit dem Parameter slices (dt. Scheiben) kann man einstellen, wie viele Unterteilungen linear_extrude entlang der Höhe vornehmen soll, um die Verdrehung abzubilden. Der Parameter convexity ist ein Hilfsparameter, der dafür sorgt, dass die Vorschau der Geometrie sauber berechnet wird und keine Löcher hat. Standardmäßig hat dieser Parameter den Wert 1. Sollte man in der Vorschau Fehler in der Geometrie entdecken, lohnt es sich, diesen Parameter zu vergrößern. Ein Wert von 10 sollte in praktisch allen Fällen ausreichend sein.
Nun werden wir die zulaufende Form des Lüfterblatts mittels einer Booleschen Differenzoperation beschreiben:
module luefterrad(
/* ... */
){
module blatt() {
/* ... */
// maße der Seitenteile
seitenwinkel =
atan(
( ( aussenbreite / 2 * cos( abs( twist ) ) ) -
( innenbreite / 2 )
) / blatthoehe
);
hoehe = sin( abs( twist ) ) * aussenbreite / 2 +
materialstaerke;
breite = aussenbreite / 2 - innenbreite / 2;
tiefe =
sqrt(
pow( ( aussenbreite / 2 * cos( abs( twist ) ) ) -
( innenbreite / 2 ), 2 ) +
pow( blatthoehe, 2 )
) + materialstaerke;
difference() {
translate( [0, innenhoehe, 0] )
rotate( [-90, 0, 0] )
linear_extrude(
height = blatthoehe,
twist = twist,
slices = 10,
convexity = 10
)
square( [aussenbreite, materialstaerke], center = true );
for (i = [0 : 1])
mirror( [i, 0, 0] )
translate([
innenbreite / 2,
innenhoehe,
-hoehe
])
rotate( [0, 0, -seitenwinkel] )
translate( [0, -tiefe / 2, 0] )
cube( [breite * 2, tiefe * 1.5, 2 * hoehe] );
} // difference
}
blatt(); // debug
}
/* ... */Wir berechnen zunächst den Winkel der Seite über die Arkustangensfunktion atan. Diese bekommt als Parameter den Überstand zwischen innenbreite und der um twist gedrehten aussenbreite. Wir verwenden hier den Absolutwert (abs) von twist, um auch bei einem negativen Verwindungsparameter das gleiche Ergebnis zu erhalten. Anschließend bestimmen wir noch die minimal notwendige hoehe, breite und tiefe des Quaders, den wir vom Lüfterblatt abziehen wollen.
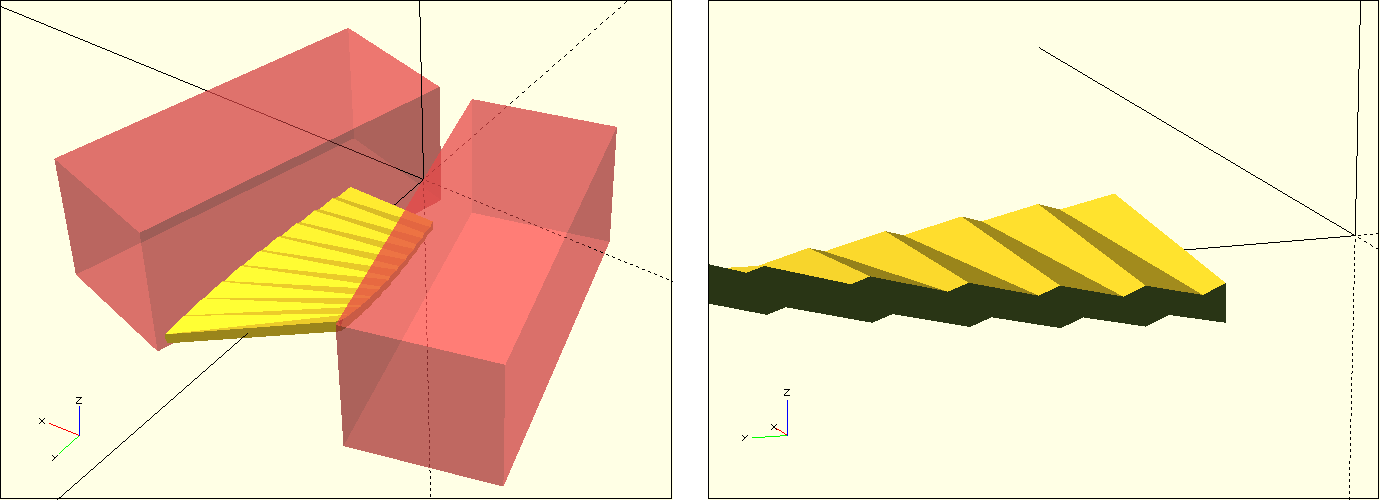
Nach diesen Vorbereitungen können wir nun unser Lüfterblatt in die Menge einer Booleschen Differenzoperation verschieben (difference) und zwei Quader definieren, die wir vom Lüfterblatt abziehen. Da die Seiten spiegelsymmetrisch sind, können wir die zwei Quader mittels einer Kombination von For-Schleife und mirror-Transformation erzeugen. Den abzuziehenden Quader machen wir etwas größer als es minimal notwendig wäre. Durch diese Zugabe decken wir auch Situationen ab, die durch eine “extreme” Parametrisierung des Lüfterrads entstehen können (z.B. bei einer sehr kleinen aussenbreite). Abbildung 12. zeigt die Position der beschriebenen Quader. Sie zeigt auch, dass nun die Seitenkanten unseres Lüfterblatts eine zackige Struktur bekommen haben. Diese zackige Struktur rührt daher, dass die 2D-Grundform unseres Blattes ein sehr dünnes Rechteck ist, welches intern nur aus zwei Dreiecken gebildet wird. Diese reichen nun nicht mehr aus, um die jetzt schrägen Seitenkanten des Lüfterblatts sauber zu beschreiben.
Wir können dieses Problem beheben, indem wir anstatt eines einfachen Rechtecks ein Polygon als 2D-Grundform verwenden, dass ausreichend viele Zwischenschritte macht. Dabei müssen wir einen kleinen Trick anwenden:
module luefterrad(
/* ... */
){
module blatt() {
/* ... */
blattunterteilung = 10;
difference() {
translate( [0, innenhoehe, 0] )
rotate( [-90, 0, 0] )
linear_extrude(
height = blatthoehe,
twist = twist,
slices = 10,
convexity = 10
)
translate([
-aussenbreite / 2,
-materialstaerke / 2
])
polygon( concat(
[for (i = [0 : blattunterteilung])
[i * aussenbreite / blattunterteilung, (i % 2) * 0.0001]
],
[for (i = [blattunterteilung : -1 : 0])
[i * aussenbreite / blattunterteilung,
materialstaerke + (i % 2) * 0.0001]
]
));
/* ... */
} // difference
}
blatt(); // debug
}
/* ... */Wir erstellen das Polygon aus zwei aneinandergehängten (concat) Feldern. Das erste Feld beschreibt die Punkte des Polygons in X-Richtung auf Höhe 0. Das zweite Feld beschreibt die Punkte des Polygons in entgegengesetzter X-Richtung auf Höhe materialstaerke. Wenn alle unsere Punkte in
Hin- und Rückrichtung exakt auf einer Linie liegen, dann wird OpenSCAD diese Punkte wegoptimieren. Damit dies nicht geschieht, müssen wir jeden zweiten Punkt minimal in Y-Richtung verschieben. Wir nutzen die Modulo-Operation für diesen Zweck. Der Ausdruck i % 2 wird für fortlaufende i abwechselnd 0 und 1. Unsere Y-Koordinate springt daher von Punkt zu Punkt zwischen 0 und 0.0001 hin und her. Hierdurch verhindern wir die Optimierung durch OpenSCAD und erzielen den gewünschten Zweck einer höheren geometrischen Auflösung unserer 2D-Grundform. Abbildung 12. zeigt, wie hierdurch die zackigen Seiten des Lüfterblatts vermieden werden.
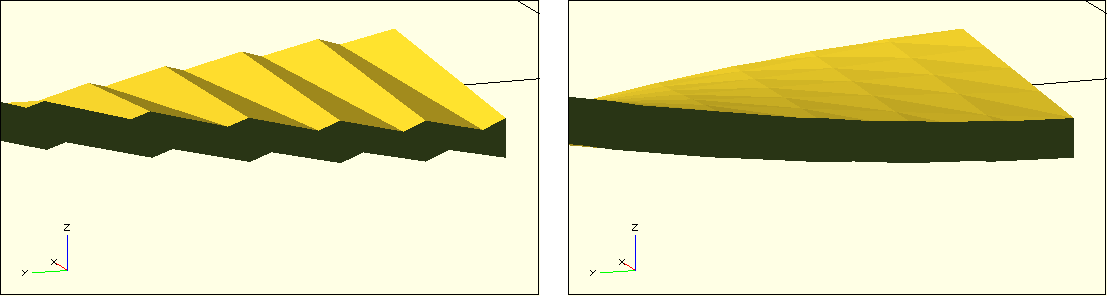
Unser Lüfterblatt ist nun fast fertig. Wir müssen es nur noch um seinen anstellwinkel drehen und den Außen- sowie Innenradius der Geometriebeschreibung hinzufügen. Für den Außenradius können wir dies mit der Booleschen Schnittoperation (intersection) und für den Innenradius mit einer weiteren Booleschen Differenzoperation (difference) erreichen:
module luefterrad(
/* ... */
){
module blatt() {
/* ... */
difference(){
intersection(){
rotate( [0, -anstellwinkel, 0] )
difference() {
/* ... */
}
// Aussenradius
translate( [0, 0, -hoehe] )
cylinder(
r = aussenradius,
h = 2 * hoehe,
$fn = 100
);
}
// Innenradius
translate( [0, 0, -hoehe] )
cylinder( r = innenradius, h = 2 * hoehe, $fn = 50);
}
}
blatt(); // debug
}
/* ... */Wir wenden die Schnitt- und Differenzoperation erst nach der Drehung um anstellwinkel an, damit die Außen- und Innenkanten des Lüfterblatts unabhängig vom anstellwinkel senkrecht bleiben. Damit ist unser Untermodul blatt vollständig beschrieben (Abbildung 12.).
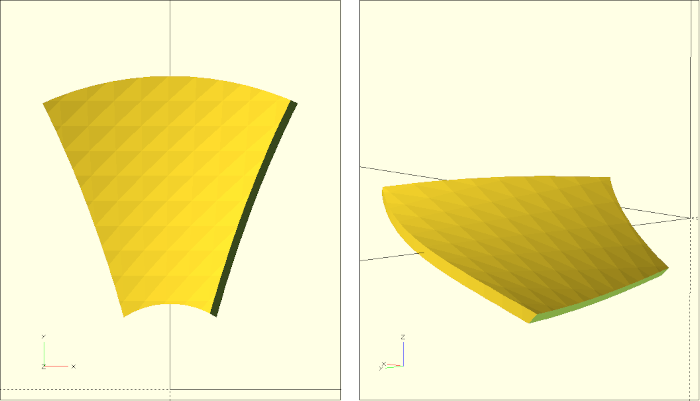
Die Fertigstellung des Hauptmoduls ist nun relativ überschaubar:
module luefterrad(
/* ... */
){
module blatt() {
}
// nabe
naben_hoehe =
sin( abs( anstellwinkel ) ) * innenbreite / 2 +
materialstaerke;
translate( [0, 0, -naben_hoehe] )
cylinder( r = innenradius, h = naben_hoehe * 2, $fn = 50);
// blaetter
for(i = [0 : 360 / blaetter : 359])
rotate( [0, 0, i] )
blatt();
}
/* ... */Wir bestimmen zunächst die Höhe unserer Nabe (naben_hoehe) in Abhängigkeit des Anstellwinkels, der Innenbreite und der Materialstärke. Anschließend erstellen wir die Nabe als einfachen Zylinder (cylinder) und zentrieren diesen Zylinder entlang der Z-Achse (translate). Die Blätter beschreiben wir nun mittels einer For-Schleife, bei der sich die Schrittweite der Schleifenvariablen i aus der parametrisierten Anzahl der Blätter ergibt (360 / blaetter). Wir nutzen die Schleifenvariable i, um unser Untermodul blatt mit entsprechend vielen Kopien über 360 Grad hinweg mittels Rotation um die Z-Achse (rotate( [0, 0, i] )) zu verteilen.

Damit ist unser Lüfterrad fertig (Abbildung 12.)!
Die Blätter des Lüfterrads haben insbesondere nach außen hin einen starken Überhang. Hier empfehlt es sich, mit einer geringen Schichtdicke (engl. layer height) und größerer Linienbreite (line width) zu drucken. Wenn ihr 3D-Drucker eine 0.4mm Druckdüse besitzt, können sie ohne Probleme Linien mit einer Breite von 0.5mm bis 0.6mm drucken. Als Schichtdicke kann man bei den meisten Druckern bis auf 0.075mm runter gehen. Ein weiterer Trick ist die Verlangsamung der Druckgeschwindigkeit für die äußeren Wandungen des Drucks (engl. outer wall speed). Hierdurch kann das Filament stärker abkühlen, da es länger dem Gebläse des Druckkopfes ausgesetzt ist.
Wenn Sie das Lüfterrad mit Stützstrukturen (engl. support) drucken, dann sollten Sie die Option für die Ausbildung eines support roofs aktivieren. Damit wird die Trennschicht zwischen Stützstruktur und 3D-Modell sauberer. Eine Alternative zur Verwendung von Stützstrukturen besteht darin, das Lüfterrad mit einer Booleschen Schnittoperation in eine obere und eine untere Hälfte zu zerteilen:
// obere Hälfte
intersection() {
luefterrad();
translate([-100,-100,0])
cube([200,200,100]);
}
// untere Hälfte
translate([120,0,0])
rotate([180,0,0])
intersection() {
luefterrad();
translate([-100,-100,-100])
cube([200,200,100]);
}Nach dem Druck beider Hälften kann man diese dann miteinander Verkleben. Dies geht zum Beispiel mit Sekundenkleber und Aktivator, oder mit einem Zweikomponentenkleber. Um eine saubere Ausrichtung der beiden Hälften zu gewährleisten, kann es hilfreich sein, zwei Bohrungen mittels Boolescher Differenzoperation in die Nabe zu legen und beim verkleben zwei Stifte in diese Bohrungen einzusetzen und als Ausrichtungshilfen zu verwenden.