

Parabolspiegel sind faszinierend. Sie bündeln einfallendes paralleles Licht bzw. elektromagnetische Strahlung in einem Fokuspunkt. Satellitenantennen oder Solarkocher machen sich diese Eigenschaft zu nutze. In die andere Richtung, wenn eine Lichtquelle im Fokuspunkt sitzt, kann man mit einem Parabolspiegel einen parallelen Lichtkegel erzeugen.
In diesem Projekt werden wir die Geometriebeschreibung für einen Parabolspiegel erstellen.
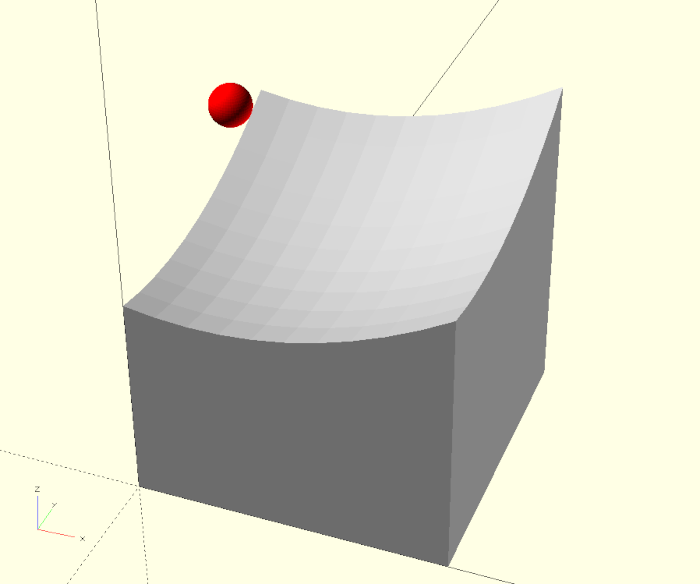
Wir werden die 3D-Grundform polyhedron kennenlernen. Sie ist im Prinzip das dreidimensionale Gegenstück zur 2D-Grundform polygon. Ein polyhedron zu erstellen ist in der Theorie einfach, in der Praxis jedoch durchaus anspruchsvoll. Daher werden wir Schritt für Schritt vorgehen und uns in diesem Projekt rein auf diese eine Neuheit konzentrieren.
Eine Parabel ist dadurch charakterisiert, dass alle Punkte auf der Parabeloberfläche den gleichen Abstand zu einer Referenz- bzw. Basisfläche und einem Fokuspunkt haben. Abbildung 11. zeigt dies exemplarisch für einen einzelnen Punkt p der Parabeloberfläche und den zugehörigen Punkten b auf der Basisfläche und f, dem Fokuspunkt. Man erkennt, dass die Punkte p, b und f ein gleichschenkliges Dreieck bilden und daher der Abstand zwischen p und f und der Abstand zwischen p und b gleich ist.
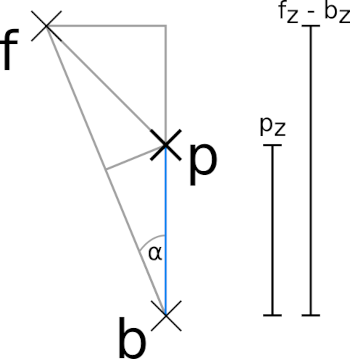
Wenn wir nun die Geometrie einer Parabel beschreiben wollen, müssen wir die Punkte p der Parabeloberfläche für einen gegebenen Fokuspunkt und eine gegebenen Basisebene herausbekommen. Wenn wir uns noch einmal Abbildung 11. anschauen, dann sehen wir, dass der Punkt p senkrecht über Punkt b steht. Denkt man sich Punkt b als Teil einer Basisfläche in der X-Y-Ebene, dann können wir die X- und Y- Koordinaten von Punkt p einfach direkt aus Punkt b übernehmen. Es bleibt also nur die Z-Koordinate von p übrig, die wir herausbekommen müssen. Hierbei können uns zwei Dreiecke helfen, die sich in Abbildung 11. verstecken. Beide Dreiecke teilen sich den Winkel α. Das größere von beiden hat seine Hypothenuse von f nach b und die Ankathete f.z - b.z. Das kleinere Dreieck hat als Hypothenuse die gesuchte Länge p.z und als Ankathete genau die Hälfte der Strecke von f nach b (weil es Teil des gleichschenkliges Dreiecks ist).
Wenn wir uns daran erinnern, dass cos(α) = Ankathete / Hypothenuse ist, ergibt sich daraus für das große Dreieck:
// Abstand zwischen f und b
abst_fb = norm(f - b)
cos(α) = (f.z - b.z) / abst_fbFür das kleine Dreieck gilt:
cos(α) = (abst_fb / 2) / p.zDa es sich in beiden Fällen um das gleiche α handelt, können wir die beiden Seitenverhältnisse gleich setzen und nach dem gesuchten p.z umformen:
(f.z - b.z) / abst_fb = (abst_fb / 2) / p.z
// beide Seiten mal p.z
p.z * (f.z - b.z) / abst_fb = abst_fb / 2
// beide Seiten durch ((f.z - b.z) / abst_fb)
p.z = (abst_fb / 2) / ((f.z - b.z) / abst_fb)
// äußere Division ersetzen durch Multiplikation mit Kehrwert
p.z = (abst_fb / 2) * (abst_fb / (f.z - b.z))
// Ausmultiplizieren: Zähler mal Zähler, Nenner mal Nenner
p.z = (abst_fb * abst_fb) / (2 * (f.z - b.z))Damit wären wir fertig! Wir haben jetzt eine kompakte Formel, um einen Punkt p auf der Parabeloberfläche in Bezug zu einem Fokuspunkt und einem Basispunkt zu berechnen. Lassen Sie uns dieses Ergebnis in einer OpenSCAD-Funktion parabelpunkt festhalten:
function parabelpunkt( fokuspunkt, basispunkt ) =
let ( abst_fb = norm(fokuspunkt - basispunkt) )
[
basispunkt.x,
basispunkt.y,
( abst_fb * abst_fb ) / ( 2 * (fokuspunkt.z - basispunkt.z) )
];Nach diesen Vorbereitungen können wir mit der Definition eines Moduls parabel beginnen und mit Hilfe unserer Funktion parabelpunkt die Punkte auf der Oberfläche der Parabel berechnen:
/*
Modul parabel
- fokuspunkt, Position des Fokuspunktes als 3D Vektor
- basis, Dimension der Basisfläche als 2D Vektor
- aufloesung, Anzahl Gitterpunkte in X- und Y-Richtung als 2D Vektor
*/
module parabel( fokuspunkt, basis, aufloesung = [10, 10] ) {
function parabelpunkt( fokuspunkt, basispunkt ) =
let ( abst_fb = norm(fokuspunkt - basispunkt) )
[
basispunkt.x,
basispunkt.y,
( abst_fb * abst_fb ) / ( 2 * (fokuspunkt.z - basispunkt.z) )
];
parabelpunkte = [
for (
y = [0 : basis.y / aufloesung.y : basis.y + 0.1],
x = [0 : basis.x / aufloesung.x : basis.x + 0.1]
)
parabelpunkt( fokuspunkt, [x,y,0] )
];
}
parabel(
fokuspunkt = [75,75,100],
basis = [150,150]
);Unser Modul parabel hat drei Parameter. Der Parameter fokuspunkt bestimmt die Position des Fokuspunktes der Parabel als dreidimensionalen Vektor. Der Parameter basis legt die Dimension der Basisfläche in Form eines zweidimensionalen Vektors fest. Wir gehen also davon aus, dass unsere Basisfläche mit einer Ecke im Ursprung liegt und sich auf der X-Y-Ebene befindet (Z = 0). Der dritte Parameter aufloesung bestimmt die Anzahl der Einzelflächen in X- und Y-Richtung, aus der die Parabeloberfläche bestehen soll.
Innerhalb des Moduls berechnen wir die parabelpunkte als Feld von Vektoren über eine generative, zweidimensionale For-Schleife. Die Schrittweite der Schleifenvariablen ergibt sich aus der jeweiligen Anzahl der Teilflächen (aufloesung) und der Dimension der Basisfläche (basis). Die Zugabe von einem zehntel Millimeter bei den jeweiligen Obergrenzen der Spannen dient der Kompensation von Rundungsfehlern. Es bedeutet nicht, dass die Parabel einen Zehntel größer würde. Innerhalb der generativen For-Schleife nutzen wir schließlich unsere Funktion parabelpunkt um jeden Punkt der Parabeloberfläche auszurechnen.
Da wir einen dreidimensionalen Körper erstellen wollen, benötigen wir noch die Punkte der Basisfläche selbst. Diese können wir ebenfalls mit einer generativen For-Schleife erzeugen. Anstelle eine Funktion wie parabelpunkt zu nutzen, können wir in diesem Fall den dreidimensionalen Vektor der Punkte direkt angeben. Er besteht lediglich aus den X- und Y-Koordinaten sowie einer konstanten Z-Koordinate, die wir auf 0 setzen:
module parabel( fokuspunkt, basis, aufloesung = [10, 10] ) {
/* ... */
parabelpunkte = [
for (
y = [0 : basis.y / aufloesung.y : basis.y + 0.1],
x = [0 : basis.x / aufloesung.x : basis.x + 0.1]
)
parabelpunkt( fokuspunkt, [x,y,0] )
];
basispunkte = [
for (
y = [0 : basis.y / aufloesung.y : basis.y + 0.1],
x = [0 : basis.x / aufloesung.x : basis.x + 0.1]
)
[x, y, 0]
];
}
/* ... */Jetzt kommen wir zum etwas kniffligen Teil. Wir müssen nun die einzelnen Flächen unserer Geometrie explizit angeben. Jede Einzelfläche benötigt vier Punkte, die reihum angegeben werden müssen. Dies ist im Grunde so, als würde man die Außenkante der Fläche mit einem Stift durchgehend und ohne neu anzusetzen nachzeichnen wollen. Sie erinnern sich vielleicht noch an diese Rätselbilder in ihrer Kindheit. Man bekam ein Blatt mit nummerierten Punkten und musste dann die Punkte nacheinander verbinden, um das Motiv zum Vorschein zu bringen. Wir machen jetzt sowas ähnliches.
Die Punkte in unseren Feldern parabelpunkte und basispunkte liegen ja nacheinander wie in einer langen Liste vor. Jede dieser Listen enthält (aufloesung.x + 1) * (aufloesung.y + 1) Punkte. Damit kann man jeden Punkt mit einer Nummer identifizieren. So wie die Hausnummern entlang einer Straße. Mit diesen “Hausnummern” der Punkte können wir jetzt eine Fläche beschreiben, indem wir jeweils vier “Hausnummern” in einem vierdimensionalen Vektor zusammenfassen:
module parabel( fokuspunkt, basis, aufloesung = [10, 10] ) {
/* ... */
anzahl_x = aufloesung.x + 1;
parabel_flaechen = [
for (
y = [0 : aufloesung.y - 1],
x = [0 : aufloesung.x - 1]
)
[
y * anzahl_x + x,
y * anzahl_x + x + 1,
(y+1) * anzahl_x + x + 1,
(y+1) * anzahl_x + x
]
];
}
/* ... */Da wir unsere Parabelpunkte zeilenweise definiert haben, liegen die Punkte im eindimensionalen Feld parabelpunkte entsprechend zeilenweise hintereinander. Die Nummern benachbarter Punkte in X-Richtung unterscheiden sich daher immer nur um 1. Die Nummern benachbarter Punkte in Y-Richtung unterscheiden sich hingegen um anzahl_x = aufloesung.x + 1. Anders ausgedrückt: alle anzahl_x Punkte im Feld parabelpunkte startet eine neue Zeile. Abbildung 11. zeigt diesen Zusammenhang für eine Auflösung von 5 x 5 Flächen schematisch auf. In diesem Beispiel wäre also aufloesung.x = 5 und dementsprechend anzahl_x = 6. Die Zeilen fangen also bei 0, 6, 12, usw. an.
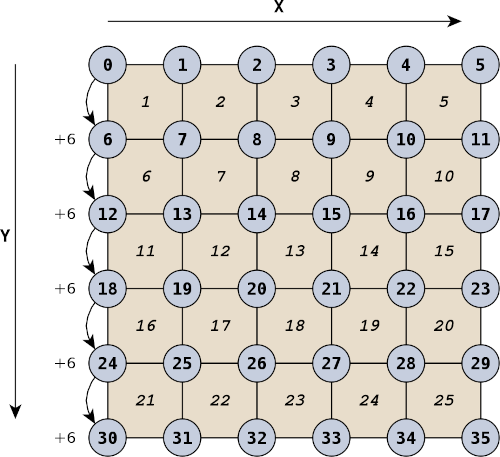
Wenn wir also die Nummer des ersten Punktes einer Fläche finden wollen, müssen wir zunächst die Startnummer der Zeile ausrechnen (y * anzahl_x) und dann die X-Position des Punktes dazurechnen (+ x). Der nächste Punkt der Fläche liegt direkt daneben. Man muss also zu der bisherigen Nummer nur 1 dazuzählen (y * anzahl_x + x + 1). Der dritte Punkt liegt eine Zeile tiefer (y + 1). Daher ist seine Nummer (y + 1) * anzahl_x + x + 1. Der vierte Punkt liegt in der gleichen Zeile vor dem dritten Punkt. Wir müssen also von der Nummer des dritten Punktes wieder 1 abziehen ((y + 1) * anzahl_x + x). Wenn wir dies für alle Flächen wiederholen, erhalten wir die gewünschte Liste der parabel_flaechen.
Für die Flächen der Basis können wir auf ähnliche Weise verfahren:
module parabel( fokuspunkt, basis, aufloesung = [10, 10] ) {
/* ... */
anzahl_x = aufloesung.x + 1;
/* ... */
anzahl_parabelpunkte = len( parabelpunkte );
basis_flaechen = [
for (
y = [0 : aufloesung.y - 1],
x = [0 : aufloesung.x - 1]
)
[
y * anzahl_x + x + anzahl_parabelpunkte,
y * anzahl_x + x + 1 + anzahl_parabelpunkte,
(y+1) * anzahl_x + x + 1 + anzahl_parabelpunkte,
(y+1) * anzahl_x + x + anzahl_parabelpunkte
]
];
}
/* ... */Da wir später die basispunkte an die parabelpunkte anfügen werden, verschieben sich die Nummern der Basispunkte um die Anzahl der Parabelpunkte. Diese Verschiebung wird durch die Addition von anzahl_parabelpunkte erreicht. Ansonsten ändert sich an der Bestimmung der Flächen nichts.
Wir haben nun die Flächen der Parabel und der Basis definiert. Was uns noch fehlt sind die Flächen der Seiten. Fangen wir mit einer Seite an:
module parabel( fokuspunkt, basis, aufloesung = [10, 10] ) {
/* ... */
anzahl_x = aufloesung.x + 1;
/* ... */
anzahl_parabelpunkte = len( parabelpunkte );
/* ... */
seiten_flaechen_1 = [
for ( x = [0 : aufloesung.x - 1] )
[
x,
x + 1,
x + 1 + anzahl_parabelpunkte,
x + anzahl_parabelpunkte
]
];
}
/* ... */Für die erste Seite laufen wir nur einmal entlang der X-Richtung und verbinden jeweils paarweise die Punkte aus dem Feld parabelpunkte mit ihren korrespondierenden Punkten aus dem Feld basispunkte. Da die Nummern der basispunkte bei anzahl_parabelpunkte beginnen, finden wir die entsprechende Addition bei den Punkten 3 und 4 der Fläche.
Die gegenüberliegende Seite kann auf ähnliche Weise beschrieben werden. Hier müssen wir die Nummern so verschieben, dass wir nicht entlang der ersten Zeile laufen, sondern entlang der letzten Zeile:
module parabel( fokuspunkt, basis, aufloesung = [10, 10] ) {
/* ... */
anzahl_x = aufloesung.x + 1;
/* ... */
anzahl_parabelpunkte = len( parabelpunkte );
/* ... */
letzte_zeile = aufloesung.y * anzahl_x;
seiten_flaechen_2 = [
for ( x = [0 : aufloesung.x - 1] )
[
letzte_zeile + x,
letzte_zeile + x + 1,
letzte_zeile + x + 1 + anzahl_parabelpunkte,
letzte_zeile + x + anzahl_parabelpunkte
]
];
}
/* ... */Wir erreichen dies, indem wir die Startnummer der letzten Zeile ausrechnen (letzte_zeile = aufloesung.y * anzahl_x;) und bei jedem Punkt der Fläche hinzuaddieren. Ansonsten bleibt alles genauso wie bei Seitenfläche 1.
Nun kommen wir zu den anderen beiden Seitenflächen. Für diese müssen wir nicht entlang der äußeren Zeilen, sondern entlang der äußeren Spalten laufen:
module parabel( fokuspunkt, basis, aufloesung = [10, 10] ) {
/* ... */
anzahl_x = aufloesung.x + 1;
/* ... */
anzahl_parabelpunkte = len( parabelpunkte );
/* ... */
seiten_flaechen_3 = [
for ( y = [0 : aufloesung.y - 1] )
[
y * anzahl_x,
(y + 1) * anzahl_x,
(y + 1) * anzahl_x + anzahl_parabelpunkte,
y * anzahl_x + anzahl_parabelpunkte
]
];
letzte_spalte = aufloesung.x;
seiten_flaechen_4 = [
for ( y = [0 : aufloesung.y - 1] )
[
letzte_spalte + y * anzahl_x,
letzte_spalte + (y + 1) * anzahl_x,
letzte_spalte + (y + 1) * anzahl_x + anzahl_parabelpunkte,
letzte_spalte + y * anzahl_x + anzahl_parabelpunkte
]
];
}
/* ... */Insgesamt sehen wir bei den Seitenflächen 3 und 4 das gleiche Schema wie bei den Seitenflächen 1 und 2. Seitenflächen 4 unterscheidet sich von Seitenflächen 3 nur dadurch, dass wir die Nummern um die Startnummer der letzten Spalte verschoben haben. Während die Nummern der Punkte entlang der X-Richtung den Abstand 1 haben, haben die Nummern der Punkte entlang der Y-Richtung den Abstand anzahl_x.
Hinter die Logik der Nummerierung der Punkte zu steigen ist gerade am Anfang nicht einfach. Es hilft sehr, sich die Geometrie auf einem Blatt Papier zu skizzieren und mit den Nummern der Punkte zu beschriften. Ganz so, wie es in Abbildung 11. zu sehen ist.
Nun ist der Punkt gekommen, wo wir endlich genügend Informationen zusammengetragen haben, um unsere Geometrie mit der Grundform polyhedron zu erzeugen:
module parabel( fokuspunkt, basis, aufloesung = [10, 10] ) {
/* ... */
polyhedron(
points = concat( parabelpunkte, basispunkte ),
faces = concat( parabel_flaechen,
basis_flaechen,
seiten_flaechen_1,
seiten_flaechen_2,
seiten_flaechen_3,
seiten_flaechen_4)
);
}
/* ... */Wir nutzen die concat-Funktion, um unsere Punkt- und Flächenmengen aneinanderzuhängen und übergeben sie als Parameter points (dt. Punkte) bzw. faces (dt. Flächen) an die 3D-Grundform polyhedron. Wenn wir nun eine Vorschau berechnen (F5) sollten wir unsere Parabel endlich sehen können.
Es gibt sicherlich Anwendungsfälle, bei denen man nicht den vollen Körper unterhalb der Parabel haben möchte. Wir können unser Modul parabel an einer Stelle anpassen, um die Möglichkeit zu schaffen, nur die Parabeloberfläche selbst mit einer gegebenen Dicke zu erzeugen:
module parabel( fokuspunkt, basis, aufloesung = [10, 10], dicke = 0 ) {
/* ... */
basispunkte = [
for (
y = [0 : basis.y / aufloesung.y : basis.y + 0.1],
x = [0 : basis.x / aufloesung.x : basis.x + 0.1]
)
let ( p = parabelpunkt( fokuspunkt, [x,y,0] ) )
if (dicke > 0)
[x, y, p.z - dicke]
else
[x, y, 0]
];
/* ... */
}
/* ... */Für diese Erweiterung geben wir unserem Modul parabel einen weiteren Parameter dicke, der den Standardwert 0 erhält. Innerhalb des Moduls ändern wir die Berechnung der Basispunkte leicht ab. Mittels let berechnen wir erneut den aktuellen Oberflächenpunkt der Parabel und halten diesen in der Variable p vor. Im Anschluss führen wir eine Fallunterscheidung durch. Wenn der Parameter dicke größer null ist, dann erzeugen wir einen Basispunkt, der genau dicke vom Parabelpunkt p entfernt ist. Ansonsten, wenn dicke gleich 0 ist, erzeugen wir den Basispunkt wie gewohnt auf der X-Y-Ebene.
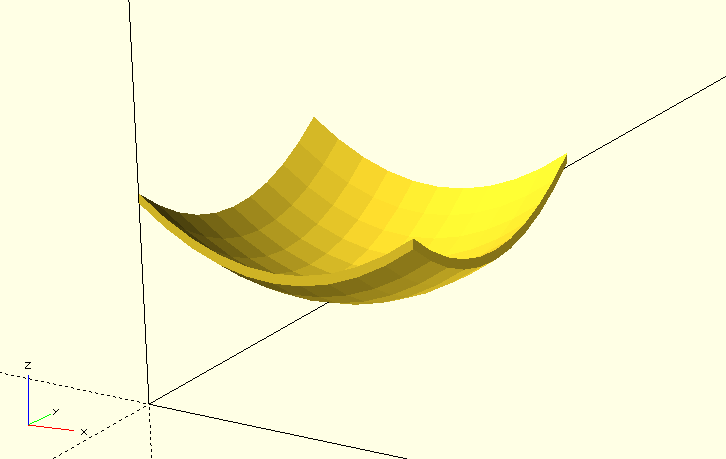
Durch diese Änderung können wir nun auch reine Parabeloberflächen ohne Unterbau erzeugen (Abbildung 11.).
Die 3D-Grundform polyhedron ist sicherlich nicht die erste Wahl, wenn man eine 3D-Geometrie mit OpenSCAD beschreiben möchte. Die Verwendung von polyhedron erfordert einiges an Vorüberlegungen und ist nicht frei von subtilen Problemen. So kann es sein, dass Flächen nicht korrekt angezeigt werden. Dies hat im Allgemeinen zwei mögliche Ursachen. Wenn die Anzeigefehler nur in der Vorschau (F5) auftreten, nicht jedoch bei der tatsächlichen Berechnung (F6), dann kann eine Erhöhung des Parameters convexity der 3D-Grundform polyhedron helfen. Standardmäßig hat dieser Parameter den Wert 1.
Die zweite Ursache für einen Anzeigefehler ist etwas mühsamer zu beheben. Die Flächen, die sie definiert haben, sind nämlich nur aus einer Richtung sichtbar. Würde man aus dem Inneren des Objektes nach Außen schauen, so könnte man durch die Flächen hindurchsehen. Welche Seite der Flächen nun sichtbar und welche nicht sichtbar ist, hängt von der Reihenfolge der Punkte ab, mit denen wir eine Fläche aufbauen. Eine Fläche mit den Punkten [0, 1, 2, 3] oder den Punkten [3, 2, 1, 0] unterscheidet sich also dadurch, ob nun Vorderseite oder Rückseite sichtbar sind. Ein gutes Hilfsmittel, um solchen Problemen zu begegnen, besteht darin, sich eine Funktion flip zu definieren, die die Reihenfolge der Elemente in einem vierdimensionalen Vektor umdreht:
function flip(vec) = [ vec[3], vec[2], vec[1], vec[0] ];Wenn dann die Darstellung einer Menge von Flächen nicht in Ordnung ist, kann man bei der Definition der Flächen die Funktion flip zum Einsatz bringen und schauen, ob sich dadurch das Problem lösen lässt. Dies sähe zum Beispiel so aus:
seiten_flaechen_1 = [
for ( x = [0 : aufloesung.x - 1] )
flip ([
x,
x + 1,
x + 1 + anzahl_parabelpunkte,
x + anzahl_parabelpunkte
])
];Insgesamt wird man die polyhedron-Grundform vermutlich eher selten verwenden. Für den Fall der Fälle stellt sie jedoch ein mächtiges Werkzeug dar, mit dem man schwierige Modellierungsaufgaben lösen kann.
Je weiter der Fokuspunkt von der Parabelform entfernt ist, desto flacher wird die Form ausfallen. In so einem Fall sollte man versuchen, die Parabel senkrecht stehend zu drucken. Hierdurch wird die Oberfläche der Parabel feiner, da 3D-Drucker üblicherweise eine höhere Auflösung in der X-Y-Ebene als in der Z-Achse haben.
Benötigen sie die Parabel mit einer anderen Außenform, z.B. rund, dann erhalten Sie diese auf einfache Weise, wenn sie die Boolesche Operation intersection mit einer passenden Grundform, z.B. einem Zylinder, verwenden.