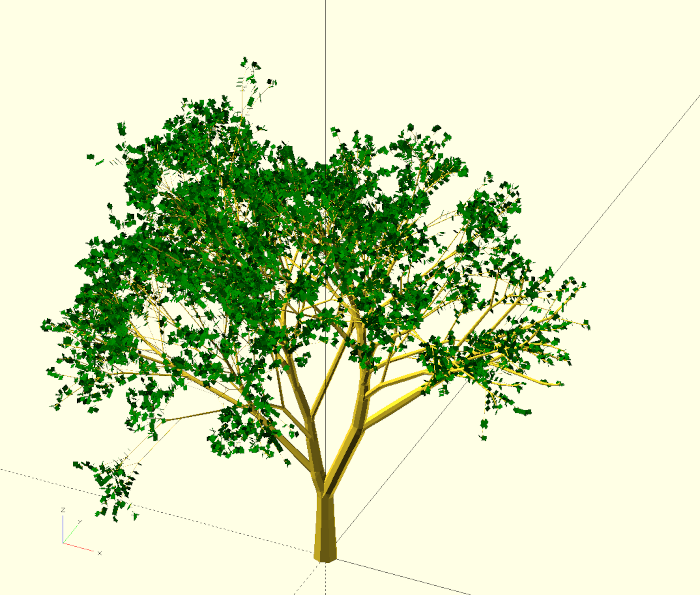
Natürliche Strukturen, wie etwa die Form von Pflanzen, entstehen vielfach aus Wachstumsprozessen, denen relativ einfache Regeln zugrunde liegen. Mittels rekursiver Geometriebeschreibungen können wir solche Wachstumsprozesse in vereinfachter Form nachbilden und so komplexe Geometrien erzeugen. In diesem Projekt wollen wir die äußere Form eines Baumes mit genau so einer rekursiven Geometriebeschreibung nachbilden.

Wir haben bereits gesehen, dass man mittels rekursiver Funktionen iterative Algorithmen in OpenSCAD definieren kann. Hier werden wir die Möglichkeit kennenlernen, Rekursion auch in der Geometriebeschreibung selbst zu verwenden. Darüber hinaus werden wir lernen, wie wir Zufallszahlen mit der Methode rands erzeugen können.
Gleich vorab muss eine Warnung ausgesprochen werden: rekursive Geometrien können in ihrer Komplexität sehr schnell anwachsen und bringen praktisch jedes Computersystem sehr schnell an seine jeweiligen Grenzen. Insbesondere die sogenannte Rekursionstiefe, die ein Parameter jeder rekursiven Geometriebeschreibung ist, ist an dieser Stelle ausschlaggebend. Beim nachfolgenden Design sollten sie diesen Parameter nur äußerst zurückhaltend ändern.
Die Grundidee für unseren rekursiven Baum besteht darin, wie bei einem Wachstumsprozess den Baum schrittweise in die Höhe wachsen zu lassen. Jeder Schritt wird dabei rekursiv erfolgen. Starten wir mit einer minimalen Geometriebeschreibung:
module r_baum(
h_schrittweite,
haupt_tiefe
){
linear_extrude( height = h_schrittweite )
children(0);
if (haupt_tiefe > 0) {
translate( [0, 0, h_schrittweite] )
r_baum(
h_schrittweite,
haupt_tiefe - 1
){
children(0);
}
}
}
r_baum(
h_schrittweite = 10,
haupt_tiefe = 20
) {
circle( d = 10, $fn=8 );
}Das Modul r_baum hat zunächst zwei Parameter h_schrittweite und haupt_tiefe. Die h_schrittweite gibt die Höhe an, um die wir in jedem Schritt wachsen wollen. Die haupt_tiefe gibt an, wie viele Schritte wir für den aktuellen Abschnitt des Baumes noch gehen können. Innerhalb des Moduls erzeugen wir zunächst ein Stück des Baumes mittels linearer Extrusion (linear_extrude) der dem Modul als erstes Element übergebenen Geometrie. Anschließend überprüfen wir, ob wir noch weitere Wachstumsschritte zur Verfügung haben (if (haupt_tiefe > 0) ...). Wenn dem so ist, dann definieren wir als weitere, um h_schrittweite nach oben verschobene Geometrie das Modul r_baum erneut. Diese rekursive Definition kopiert im Prinzip die Modulbeschreibung des Moduls r_baum erneut an diese Stelle. Dies ist ein wenig so, wie der Effekt, wenn man in zwei gegenüberliegende Spiegel schaut. Es entsteht eine endlose Folge von Kopien.
Damit diese Folge von Kopien in unserer Modulbeschreibung eben nicht endlos ist, ist der Parameter haupt_tiefe so wichtig. Bei der rekursiven Definition von r_baum reduzieren wir die haupt_tiefe um 1. Auf diese Weise wird haupt_tiefe bei jedem Kopierschritt etwas geringer, bis schließlich haupt_tiefe den Wert 0 annimmt und das Kopieren stoppt. Zusätzlich reichen wir mit children(0) die dem Modul ursprünglich übergebene Geometrie an die rekursive Kopie weiter.
Als nächstes wollen wir in unserer Modulbeschreibung die Möglichkeit zufälliger Variationen anlegen. Dies können wir durch die Funktion rands erreichen:
module r_baum(
h_schrittweite,
haupt_tiefe,
z_init
){
zufall = rands( 0, 1, 10, z_init );
linear_extrude( height = h_schrittweite )
children(0);
if (haupt_tiefe > 0) {
translate( [0, 0, h_schrittweite] )
r_baum(
h_schrittweite,
haupt_tiefe - 1 - zufall[0] * 2,
zufall[9] * 100
) {
children(0);
}
}
}
r_baum(
h_schrittweite = 10,
haupt_tiefe = 20,
z_init = 42
) {
circle( d = 10, $fn=8);
}Die Funktion rands (kurz für engl. random values -> dt. Zufallszahlen) erzeugt ein Feld von Zufallszahlen. Die ersten beiden Parameter geben die untere und obere Schranke dieser Zahlen an. In unserem Fall erzeugen wir also zufällige Kommazahlen zwischen 0 und 1. Der dritte Parameter gibt an, wie viele Zufallszahlen das Feld enthalten soll. Wir lassen uns erstmal 10 Zahlen erzeugen, da wir an verschiedenen Stellen innerhalb unseres Moduls “Zufall” einstreuen werden. Der letzte Parameter ist ein Initialisierungswert, den wir von außen über den Modulparameter z_init definieren. Die Zufallszahlen, die die Funktion rands erzeugt, sind nicht wirklich zufällig. Sie sehen nur so aus. In Wirklichkeit sind es nur Pseudozufallszahlen, die eine feste Reihenfolge haben. Der Initialisierungswert (eine beliebige Zahl), legt diese Reihenfolge fest. Dies hat den Vorteil, dass wir mit verschiedenen Initialisierungswerten unterschiedliche Folgen von Zufallszahlen bekommen, gleichzeitig jedoch auch die Kontrolle über die Zufallsfolgen behalten. Wenn wir den Initialisierungswert nicht ändern, erhalten wir immer die selbe Folge an Zahlen. Ganz konkret bedeutet das für unseren Baum, dass wir den Parameter z_init unseres Moduls ändern können, um eine neue Baumvariante zu generieren. Wenn uns die Variante gefällt, können wir uns den Wert von z_init merken und so die jeweilige Variante gezielt erzeugen. Wäre dies nicht der Fall und die Zufallszahlen wirklich zufällig, würden wir bei jeder Berechnung der Geometrie einen anderen Baum erhalten.
In unserem Modul r_baum nutzen wir die Zufallszahlen an zwei Stellen. Zum einen reduzieren wir die haupt_tiefe bei der rekursiven Definition von r_baum nicht nur um eins, sondern zusätzlich auch noch um einen zufälligen Wert zwischen 0 und 2 (zufall[0] * 2). Wir nutzen hierzu die erste unserer zehn Zufallszahlen. Zum anderen übergeben wir die letzte unserer zehn Zufallszahlen als neuen z_init-Wert an die rekursive Instanz weiter. Wir skalieren den Wert auf einen Bereich zwischen 0 und 100, da die Dokumentation von rands an dieser Stelle etwas unklar ist, ob sie ganze Zahlen oder Kommazahlen als Initialisierungswert benötigt. Mit der Skalierung gehen wir hier einfach auf Nummer sicher. Wenn Sie nun in der Testinstanz des Moduls r_baum den Wert von z_init ändern und eine Vorschau berechnen (F5), dann werden sie sehen, wie sich die Höhe unseres “Baumes” mit jedem Wert von z_init zufällig ändert.
Stamm und Äste von Bäumen sind überwiegend grade, weisen jedoch durchaus Variationen in ihrer Dicke auf und werden in Wachstumsrichtung dünner. Dies können wir über einen Skalierungsparameter modellieren:
module r_baum(
h_schrittweite,
haupt_tiefe,
z_init,
skalierung,
s_varianz
){
zufall = rands( 0, 1, 10, z_init );
function z(von, bis, idx) = zufall[idx] * (bis - von) + von;
sf = skalierung + z(-1, 1 ,1) * s_varianz;
linear_extrude( height = h_schrittweite, scale = sf )
children(0);
if (haupt_tiefe > 0) {
translate( [0, 0, h_schrittweite] )
r_baum(
h_schrittweite,
haupt_tiefe - 1 - z(0,2,0),
z(0,100,9),
skalierung,
s_varianz
) {
scale( [sf, sf] )
children(0);
}
}
}
r_baum(
h_schrittweite = 10,
haupt_tiefe = 20,
z_init = 42,
skalierung = 0.97,
s_varianz = 0.1
) {
circle( d = 10, $fn=8);
}Wir haben unserem Modul r_baum zwei neue Parameter hinzugefügt. Der Parameter skalierung gibt an, auf wieviel Prozent die übergeben Grundform in jedem Schritt schrumpfen soll. Der Parameter s_varianz definiert die zufällige Schwankungsbreite der skalierung. Innerhalb des Moduls haben wir zunächst ein wenig aufgeräumt und eine Funktion z definiert, die uns einen Zufallswert aus dem Feld zufall liefert und diesen auf ein Intervall [von,bis] skaliert. Hierdurch wird die weitere Verwendung von Zufallszahlen in unserem Modul etwas angenehmer. Im Anschluss bestimmen wir einen Skalierungsfaktor sf aus den Parametern skalierung und s_varianz, der für diesen Schritt der Rekursion gelten soll. Wir übergeben sf der linearen Extrusion (linear_extrude) als Parameter scale. Damit der nächste Baumabschnitt nun sauber an die skalierte Grundform anschließt, müssen wir diese bei der Weitergabe an die rekursive Definition von r_baum entsprechend skalieren (scale( [sf, sf] )).
Unser Baum ist derzeit nichts mehr als ein einzelner Ast. Um dies zu ändern, müssen wir während unseres simulierten Wachstumsprozesses irgendwann (mindestens) einen weiteren Ast abzweigen. Damit wir dies nicht unendlich oft machen, müssen wir eine weitere Rekursionstiefe abzeig_tiefe für diesen neuen Rekursionspfad einführen:
module r_baum(
h_schrittweite,
ht_init,
haupt_tiefe,
z_init,
skalierung,
s_varianz,
at_init,
abzweig_tiefe,
abzweig_winkel
){
/* ... */
linear_extrude( height = h_schrittweite, scale = sf )
children(0);
// Sollen wir abzweigen?
if (
(abzweig_tiefe > 0) &&
(z(0, 0.8 ,2) < ((ht_init - haupt_tiefe) / ht_init) )
){
r_winkel = z(0, 720, 3);
a_winkel = abzweig_winkel / 2 + z(0, 0.5, 4) * abzweig_winkel;
translate( [0, 0, h_schrittweite] )
rotate( [0, 0, r_winkel] )
rotate( [a_winkel, 0, 0] )
r_baum(
h_schrittweite,
ht_init,
haupt_tiefe,
z(0,100, 5),
skalierung,
s_varianz,
at_init,
abzweig_tiefe - 1,
abzweig_winkel
) {
scale( [sf, sf] )
children(0);
}
}
if (haupt_tiefe > 0) {
translate( [0, 0, h_schrittweite] )
r_baum(
h_schrittweite,
ht_init,
haupt_tiefe - 1 - z(0,2,0),
z(0,100, 9),
skalierung,
s_varianz,
at_init,
abzweig_tiefe,
abzweig_winkel
) {
scale( [sf, sf] )
children(0);
}
}
}
r_baum(
h_schrittweite = 10,
ht_init = 20,
haupt_tiefe = 20,
z_init = 42,
skalierung = 0.97,
s_varianz = 0.1,
at_init = 1,
abzweig_tiefe = 1,
abzweig_winkel = 30
) {
circle( d = 10, $fn=8);
}Wir haben unser Modul r_baum um einige Parameter erweitert. Die beiden Init-Parameter ht_init und at_init enthalten die initialen Werte der Parameter haupt_tiefe und abzweig_tiefe. Wir benötigen diese initialen Werte, um bei einer Abzweigung mit einem neuen Ast “frisch” starten zu können. Darüber hinaus haben wir den Parameter abzweig_winkel eingeführt, mit dem wir den (maximalen) Winkel der abzweigenden Äste definieren.
Nach der Geometrie des Astabschnitts (linear_extrude ...) entscheiden wir uns, ob an dieser Stelle ein neuer Ast abzweigen soll. Wir tun dies nur, wenn zwei Bedingungen erfüllt sind: die abzweig_tiefe muss größer 0 sein (sicheres Rekursionsende!) und (&&) ein Zufallswert zwischen 0 und 0.8 muss kleiner sein als ein bestimmtes Verhältnis zwischen aktueller Haupttiefe und initialer Haupttiefe ((ht_init - haupt_tiefe) / ht_init). Warum das? Setzen wir mal ein paar Zahlen ein, um zu sehen, wie sich das Verhältnis mit der Zeit ändert. Am Anfang ist die aktuelle haupt_tiefe gleich der initialen Haupttiefe ht_init. Damit wird das Verhältnis 0. Das ein Zufallswert aus dem Intervall 0 bis 0.8 kleiner als 0 ist, ist ausgeschlossen. Am Ende ist die aktuelle haupt_tiefe gleich 0. Dann wird das Verhältnis 1. In diesem Fall ist es garantiert, dass ein Zufallswert aus dem Intervall 0 bis 0.8 kleiner ist. Anders gesagt: je weiter unser Ast wächst, desto wahrscheinlicher ist es, dass ein neuer Ast abgezweigt wird.
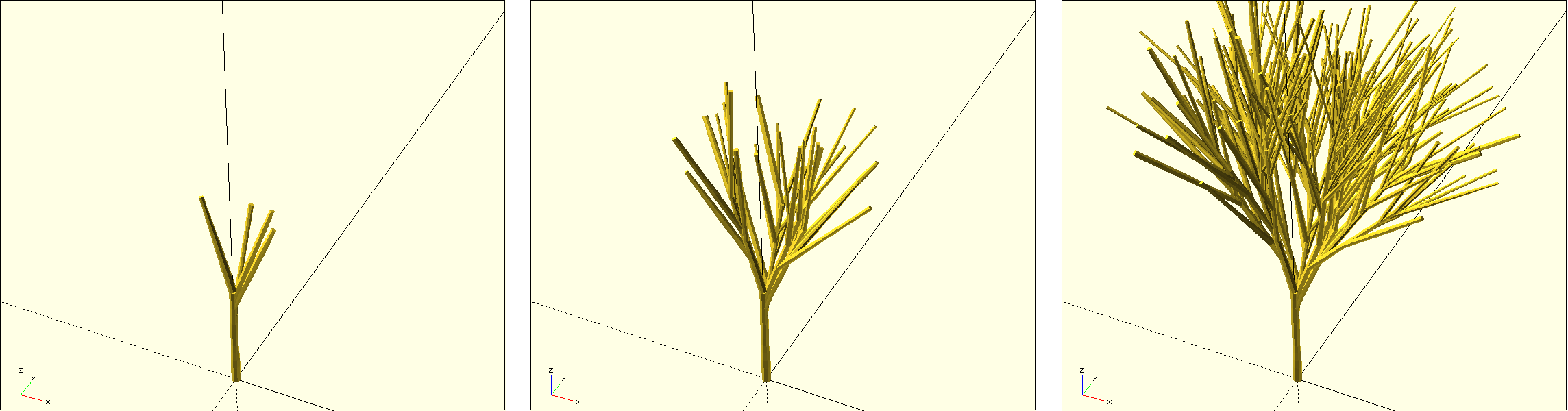
Innerhalb der If-Fallunterscheidung definieren wir zunächst die zwei Winkel r_winkel und a_winkel. Der Rotationswinkel r_winkel ist ein zufälliger Winkel, der bestimmt, in welche Richtung der Zweig abzweigen soll. Der Abzweigewinkel a_winkel bestimmt den konkreten Abzweigewinkel des Astes als eine Mischung aus dem Parameter abzweig_winkel und einem zufälligen Anteil. Anschließend wird der neue Ast als rekursive Definition des Moduls r_baum beschrieben, dass jedoch nun passend gedreht wird, bevor es um h_schrittweite verschoben wird. Die haupt_tiefe dieses neuen Astes wird auf ht_init zurückgesetzt. Die abzweig_tiefe wird hingegen um 1 verringert. Abbildung 10. zeigt die Wirkung dieses zweiten Rekursionspfades für Rekursionstiefen von 1, 2, und 3.
Unsere Zweige wirken derzeit noch etwas unrealistisch lang und sie häufen sich je nach Zufall doch irgendwie unnatürlich. Lassen Sie uns das erste Problem zuerst angehen, indem wir davon ausgehen, dass sich die Schrittweite in der Länge mit zunehmender Rekursionstiefe verringern sollte. Dies können wir über einen weiteren Parameter r_schrittweite für die Schrittweitenreduktion ermöglichen:
module r_baum(
h_schrittweite,
r_schrittweite,
ht_init,
haupt_tiefe,
z_init,
skalierung,
s_varianz,
at_init,
abzweig_tiefe,
abzweig_winkel
){
/* ... */
// Sollen wir abzweigen?
if (
(abzweig_tiefe > 0) &&
(z(0, 0.8 ,2) < ((ht_init - haupt_tiefe) / ht_init) )
){
r_winkel = z(0, 720, 3);
a_winkel = abzweig_winkel / 2 + z(0, 0.5, 4) * abzweig_winkel;
neue_schrittweite =
h_schrittweite -
h_schrittweite / 2.5 * pow(r_schrittweite, abzweig_tiefe);
translate( [0, 0, h_schrittweite] )
rotate( [0, 0, r_winkel] )
rotate( [a_winkel, 0, 0] )
r_baum(
neue_schrittweite,
r_schrittweite,
ht_init,
ht_init,
z(0,100, 5),
skalierung,
s_varianz,
at_init,
abzweig_tiefe - 1,
abzweig_winkel
) {
scale( [sf, sf] )
children(0);
}
}
if (haupt_tiefe > 0) {
translate( [0, 0, h_schrittweite] )
r_baum(
h_schrittweite,
r_schrittweite,
ht_init,
haupt_tiefe - 1 - z(0,2,0),
z(0,100,9),
skalierung,
s_varianz,
at_init,
abzweig_tiefe,
abzweig_winkel
) {
scale( [sf, sf] )
children(0);
}
}
}
r_baum(
h_schrittweite = 10,
r_schrittweite = 0.7,
/* ... */
) {
circle( d = 10, $fn=8);
}Wir nutzen für die Abnahme der Schrittweite eine Potenzfunktion. Da r_schrittweite kleiner 1 ist, machen höhere Potenzen den resultierenden Wert kleiner. Anders ausgedrückt: mit zunehmender Rekursionstiefe nimmt die Reduktion der Schrittweite zu.
Achten Sie darauf, dass sie an allen Stellen, wo sie das Modul r_baum verwenden, die Parameterlisten aktualisieren. Aufgrund eines Fehlers in OpenSCAD können wir an dieser Stelle leider keine Standardwerte für die Parameter setzen und müssen diese jedesmal vollständig angeben. Versucht man Standardparameter zu nutzen, stürzt OpenSCAD ab einer gewissen Anzahl an Parametern mit einem Speicherfehler ab.
Nun können wir uns um das zweite Problem kümmern. Die abzweigenden Äste starten mit der gleichen Größe wie der Ast, aus dem sie hervorgehen. Dies ist nicht sonderlich realistisch. Die Größe des abzweigenden Astes sollte zudem von seinem Winkel abhängen. Ist der Winkel groß, sollte der Durchmesser eher klein sein. Darüber hinaus sollte auch der Hauptast etwas von seinem Durchmesser verlieren und je nach Winkel des Abzweigenden Astes, diesem etwas ausweichen. Lassen Sie uns diese Gedanken in eine Geometriebeschreibung umsetzen:
module r_baum(
h_schrittweite,
r_schrittweite,
ht_init,
haupt_tiefe,
z_init,
skalierung,
s_varianz,
at_init,
abzweig_tiefe,
abzweig_winkel,
abzweig_min_gr,
abzweig_max_gr
){
/* ... */
// Sollen wir abzweigen?
if (
(abzweig_tiefe > 0) &&
(z(0, 0.8 ,2) < ((ht_init - haupt_tiefe) / ht_init) )
){
/* ... */
// wird 0, wenn a_winkel groß ist
// wird 1, wenn a_winkel klein ist
abzweig_verhaeltnis = (abzweig_winkel / a_winkel) - 1.0;
abzweig_skalierung =
abzweig_min_gr * abzweig_verhaeltnis +
abzweig_max_gr * (1.0 - abzweig_verhaeltnis);
haupt_skalierung =
sf * abzweig_verhaeltnis +
abzweig_max_gr * (1.0 - abzweig_verhaeltnis);
translate( [0, 0, h_schrittweite] )
rotate( [0, 0, r_winkel] )
rotate( [a_winkel, 0, 0] )
r_baum(
neue_schrittweite,
r_schrittweite,
ht_init,
ht_init,
z(0,100, 5),
skalierung,
s_varianz,
at_init,
abzweig_tiefe - 1,
abzweig_winkel,
abzweig_min_gr,
abzweig_max_gr
) {
scale( [abzweig_skalierung, abzweig_skalierung] )
children(0);
}
// in gegenrichtung gedrehter Hauptast
if (haupt_tiefe > 0) {
translate( [0, 0, h_schrittweite] )
rotate( [0, 0, r_winkel] )
rotate( [-(abzweig_winkel - a_winkel), 0, 0] )
r_baum(
neue_schrittweite,
r_schrittweite,
ht_init,
haupt_tiefe - 1 - z(0,2, 6),
z(0,100, 7),
skalierung,
s_varianz,
at_init,
abzweig_tiefe,
abzweig_winkel,
abzweig_min_gr,
abzweig_max_gr
) {
scale( [haupt_skalierung, haupt_skalierung] )
children(0);
}
}
} else {
if (haupt_tiefe > 0) {
translate( [0, 0, h_schrittweite] )
r_baum(
h_schrittweite,
r_schrittweite,
ht_init,
haupt_tiefe - 1 - z(0,2,0),
z(0,100,9),
skalierung,
s_varianz,
at_init,
abzweig_tiefe,
abzweig_winkel,
abzweig_min_gr,
abzweig_max_gr
) {
scale( [sf, sf] )
children(0);
}
}
}
}
r_baum(
/* ... */
abzweig_min_gr = 0.3,
abzweig_max_gr = 0.8
) {
circle( d = 10, $fn=8);
}Die Geometriebeschreibung ist um einiges umfangreicher geworden! Wir haben zwei neue Parameter abzweig_min_gr und abzweig_max_gr hinzugefügt. Diese bestimmen, in welchem Größenbereich sich abzweigende Äste im Verhältnis zur Größe des Hauptastes bewegen. Innerhalb des Moduls haben wir den Fall, in dem wir nicht abzweigen in einen else-Block gesetzt. Dies bedeutet, dass wir im Falle eines Abzweigs mit dem Hauptast nicht einfach geradeaus weiterwachsen sondern das normale Wachstum stoppen.
Innerhalb der Beschreibung der Abzweigung bestimmen wir zunächst ein abzweig_verhältnis und nutzen dies, neue Skalierungsfaktoren sowohl für den abzweigenden Ast als auch für den Hauptast (abzweig_skalierung und haupt_skalierung) zu definieren. In der nachfolgenden Definition des abzweigenden Astes wird abzweig_skalierung dann genutzt, um die weitergereichte children(0)-Geometrie zu skalieren. Nach der Definition des abzweigenden Astes folgt nun eine neue Definition des Hauptastes. Auch hier wird erst einmal geprüft, ob der Hauptast überhaupt noch fortgesetzt werden soll (if (haupt_tiefe > 0)). Im Gegensatz zum normalen Hauptast-Wachstum wird nun der Hauptast vom abzweigenden Ast weggedreht (rotate( [-(abzweig_winkel - a_winkel), 0, 0] )) und die weitergereichte Geometrie wird mit haupt_skalierung skaliert. Darüber hinaus übernimmt der Hauptast nun auch die neue_schrittweite des abzweigenden Astes. Setzt man testweise at_init und abzweig_tiefe auf 3 oder sogar 4, dann sieht man, dass wir auf dem richtigen Weg sind.

Wenn man genau hinschaut, dann sieht man, dass die Verbindungsstellen an den Astabzweigungen noch sehr grob aussehen (Abbildung 10.). Dies können wir mit Hilfe einer hull-Transformation an geeigneter Stelle lösen:
module r_baum(
/* ... */
){
/* ... */
// Sollen wir abzweigen?
if (
(abzweig_tiefe > 0) &&
(z(0, 0.8 ,2) < ((ht_init - haupt_tiefe) / ht_init) )
){
/* ... */
translate( [0, 0, h_schrittweite] )
rotate( [0, 0, r_winkel] )
rotate( [a_winkel, 0, 0] )
r_baum(
/* ... */
) {
scale( [abzweig_skalierung, abzweig_skalierung] )
children(0);
}
// Verbindung zum abzweigenden Ast glätten
hull() {
translate( [0, 0, h_schrittweite] )
linear_extrude( height = 0.01 )
scale([sf,sf])
children(0);
translate( [0, 0, h_schrittweite] )
rotate( [0, 0, r_winkel] )
rotate( [a_winkel, 0, 0] )
linear_extrude(
height = neue_schrittweite / 2,
scale = pow(skalierung,1/3)
)
scale( [abzweig_skalierung, abzweig_skalierung] )
children(0);
}
// in gegenrichtung gedrehter Hauptast
if (haupt_tiefe > 0) {
translate( [0, 0, h_schrittweite] )
rotate( [0, 0, r_winkel] )
rotate( [-(abzweig_winkel - a_winkel), 0, 0] )
r_baum(
/* ... */
) {
scale( [haupt_skalierung, haupt_skalierung] )
children(0);
}
// Verbindung zum Hauptast glätten
hull() {
translate( [0, 0, h_schrittweite] )
linear_extrude( height = 0.01 )
scale([sf,sf])
children(0);
translate( [0, 0, h_schrittweite] )
rotate( [0, 0, r_winkel] )
rotate( [-(abzweig_winkel - a_winkel), 0, 0] )
linear_extrude(
height = neue_schrittweite / 2,
scale = pow(skalierung,1/3)
)
scale( [haupt_skalierung, haupt_skalierung] )
children(0);
}
}
} else {
if (haupt_tiefe > 0) {
translate( [0, 0, h_schrittweite] )
r_baum(
h_schrittweite,
r_schrittweite,
ht_init,
haupt_tiefe - 1 - z(0,2,0),
z(0,100,9),
skalierung,
s_varianz,
at_init,
abzweig_tiefe,
abzweig_winkel,
abzweig_min_gr,
abzweig_max_gr
) {
scale( [sf, sf] )
children(0);
}
}
}
}
r_baum(
h_schrittweite = 10,
r_schrittweite = 0.7,
ht_init = 20,
haupt_tiefe = 20,
z_init = 42,
skalierung = 0.97,
s_varianz = 0.1,
at_init = 1,
abzweig_tiefe = 1,
abzweig_winkel = 30,
abzweig_min_gr = 0.3,
abzweig_max_gr = 0.8
) {
circle( d = 10, $fn=8);
}Für die Glättung instanziieren wir die übergebene Geometrie (children(0)) jeweils zwei Mal. Eine Instanz positionieren wir am Ende des aktuellen Wachstumsabschnitts und die andere Instanz positionieren wir an den Anfang der Abzweigung bzw. an den Anfang des gedrehten Hauptastes. Letzterer Instanz geben wir die Hälfte der Höhe des nächsten Wachstumsabschnitts und skalieren sie entsprechend. Anschließend nutzen wir die hull-Transformation, um beide “Baumscheiben” miteinander zu verbinden und so die vorhandenen Lücken zu überbrücken (Abbildung 10.).

Was uns jetzt noch fehlt sind die Blätter des Baumes. Hier können wir die Abzweigtiefe nutzen, um im letzten Rekursionsschritt Blätter zu zeichnen anstelle eines Astes:
module r_baum(
/* ... */
){
zufall = rands( 0, 1, 10, z_init );
function z(von, bis, idx) = zufall[idx] * (bis - von) + von;
if ((abzweig_tiefe < 1) && ($children > 1)) {
color("green")
rotate([(floor(z_init) % 2 == 0) ? 45 : -45,0,0])
linear_extrude(height = 0.1)
children(1);
} else {
/* ... */
// Sollen wir abzweigen?
if (
(abzweig_tiefe > 0) &&
(z(0, 0.8 ,2) < ((ht_init - haupt_tiefe) / ht_init) )
){
/* ... */
translate( [0, 0, h_schrittweite] )
rotate( [0, 0, r_winkel] )
rotate( [a_winkel, 0, 0] )
r_baum(
/* ... */
) {
scale( [abzweig_skalierung, abzweig_skalierung] )
children(0);
if ($children > 1) children(1);
}
// Verbindung zum abzweigenden Ast glätten
/* ... */
// in gegenrichtung gedrehter Hauptast
if (haupt_tiefe > 0) {
translate( [0, 0, h_schrittweite] )
rotate( [0, 0, r_winkel] )
rotate( [-(abzweig_winkel - a_winkel), 0, 0] )
r_baum(
/* ... */
) {
scale( [haupt_skalierung, haupt_skalierung] )
children(0);
if ($children > 1) children(1);
}
// Verbindung zum Haupt glätten
/* ... */
}
} else {
if (haupt_tiefe > 0) {
translate( [0, 0, h_schrittweite] )
r_baum(
/* ... */
) {
scale( [sf, sf] )
children(0);
if ($children > 1) children(1);
}
}
if ((abzweig_tiefe < 2) && ($children > 1)) {
color("green")
rotate([(floor(z_init) % 2 == 0) ? 45 : -45,0,0])
linear_extrude(height = 0.1)
children(1);
}
}
}
}
r_baum(
/* ... */
at_init = 4,
abzweig_tiefe = 4,
/* ... */
) {
circle( d = 10, $fn=8);
square([2,2]);
}Wir nutzen als Blätter eine weitere, von außen an unser Modul übergebene Geometrie (hier: square([2,2]);). Dementsprechend müssen wir alle rekursiven Verwendungen von r_baum innerhalb unseres Moduls aktualisieren und auch die Geometrie children(1) weiterreichen. Dies sollten wir jedoch nur tun, wenn auch wirklich eine zweite Geometrie übergeben wurde. Daher prüfen wir $children an den entsprechenden Stellen. Da die Ausbeute an Blättern etwas gering ausfällt, wenn man die Blätter nur am Ende der Rekursion zeichnet (if (abzweig_tiefe < 1)) haben wir die Blattgeometrie noch ein weiteres Mal unterhalb des regulären Wachstumspfades definiert und an dieser Stelle schon auf die vorletzte Rekursionsebene geprüft (if (abzweig_tiefe < 2)). Da man nun erst ab einer insgesamten Rekursionstiefe von etwa 4 ein schönes Blätterdach bekommt, haben wir die Parameter der Testinstanz unseres Moduls r_baum ebenfalls angepasst. Der Ausdruck (floor(z_init) % 2 == 0) ? 45 : -45 sorgt dafür, dass die Blätter mal in die eine und mal in die andere Richtung gedreht werden in Abhängigkeit davon, ob der abgerundete (floor) z_init-Wert gerade oder ungerade ist. Wir haben an dieser Stelle den Wert z_init genommen, da sich dieser beständig ändert. Wir hätten genauso gut auch einen Wert aus dem Zufallsfeld nehmen können.
Damit sind wir mit unserer Geometriebeschreibung fertig. Wenn sie automatisch ein paar zufällige Bäume erstellen wollen, dann können Sie die Testinstanz wie folgt parametrisieren:
srnd = rands(0,1000,1)[0];
echo(srnd);
r_baum(
h_schrittweite = 10,
r_schrittweite = 0.7,
ht_init = 20,
haupt_tiefe = 20,
z_init = srnd,
skalierung = 0.97,
s_varianz = 0.1,
at_init = 4,
abzweig_tiefe = 4,
abzweig_winkel = 50,
abzweig_min_gr = 0.3,
abzweig_max_gr = 0.8
) {
circle( d = 10, $fn=8);
square([2,2]);
}Die Variable srnd enthält nun eine einzelne zufällige Zahl, die sie für den Parameter z_init des Moduls r_baum nutzen. Da wir hier die rands-Funktion ohne Init-Parameter verwenden, bekommen wir bei jeder Berechnung (F5 bzw. F6) eine neue zufällige Zahl. Der echo-Befehl gibt die Zahl zudem in deŕ OpenSCAD-Konsole aus. Hierdurch kann man sich “gute” Init-Werte merken, aus denen schöne Bäume hervorgegangen sind. Es lohnt sich auch, den Parameter abzweig_winkel zu variieren. Gleiches gilt auch für at_init und abzweig_tiefe sofern es ihre Geduld und die verfügbare Rechenleistung ihres Computers zulassen. Abbildungen 10. und 10.6 zeigen zwei Bäume mit 40 bzw. 60 Grad Abzweigwinkel.