

Im überwiegenden Teil der Fälle wird OpenSCAD für die Konstruktion und die geometrische Beschreibung von technischen Systemen bzw. Bauteilen genutzt. Dies bedeutet jedoch nicht, dass sich nicht auch organische Formen mit OpenSCAD erzeugen ließen. In diesem Projekt werden wir eine Flammenskulptur erzeugen, die wir mit Hilfe einer Reihe mathematischer Funktionen modellieren werden.
Wir werden in diesem Projekt sowohl neue mathematische Funktionen von OpenSCAD kennenlernen (exp, norm, cross) als auch unsere eigenen Funktionen definieren. In diesem Zusammenhang werden wir das erste Mal eine rekursive Funktion verwenden. Desweiteren werden wir sehen, wie wir den children-Aufruf über mehrere Modulebenen kaskadieren können und was es mit dem Befehl concat auf sich hat.
Fangen wir mit der Modulbeschreibung und Testinstanz unseres Moduls an. Im Gegensatz zu den bisherigen Projekten werden wir gleich alle Parameter am Anfang definieren und nicht erst nach und nach einführen:
// Eine Flammenskulptur
module flammen(
hoehe,
skalierung_start = [1.0, 1.0, 1.0],
skalierung_end = [0.1, 0.1, 0.1],
x_radius = 15,
y_radius = 10,
steilheit = 0.2,
uebergang = 0.35,
hoehen_verzerrung = 0.7,
rotationen = 1,
ebenen = 30
) {
}
flammen( 180 ) {
circle( d = 60 , $fn = 30);
sphere( d = 60 );
}Betrachtet man die Testinstanz unseres Moduls flammen unterhalb der Modulbeschreibung, so sieht man, dass das Modul auf einer Geometriemenge operieren wird. Hierdurch kann man nachträglich die zugrunde liegenden Geometrien und somit den Charakter der Skulptur ändern.
Die Grundidee für unser Modell besteht darin, zunächst eine Menge an Positionen zu berechnen, die einen geschwungenen Pfad beschreiben und dann anschließend eine 2D-Grundform entlang dieses Pfades zu bewegen und mittels der hull-Transformation paarweise in eine 3D-Geometrie zu überführen. Zusätzlich soll die 2D-Grundform entlang des Pfades skaliert werden. Lassen Sie uns mit der Berechnung des geschwungenen Pfades beginnen:
module flammen(
hoehe,
skalierung_start = [1.0, 1.0, 1.0],
skalierung_end = [0.1, 0.1, 0.1],
x_radius = 15,
y_radius = 10,
steilheit = 0.2,
uebergang = 0.35,
hoehen_verzerrung = 0.7,
rotationen = 1,
ebenen = 30
) {
// Positionen entlang des Pfades
schrittweite = hoehe / ebenen;
rot_sw = 360 * rotationen / ebenen;
positionen = [ for (i = [0:ebenen]) [
cos( i * rot_sw) * x_radius,
sin( i * rot_sw) * y_radius,
pow( i / ebenen, hoehen_verzerrung) * hoehe
]];
}
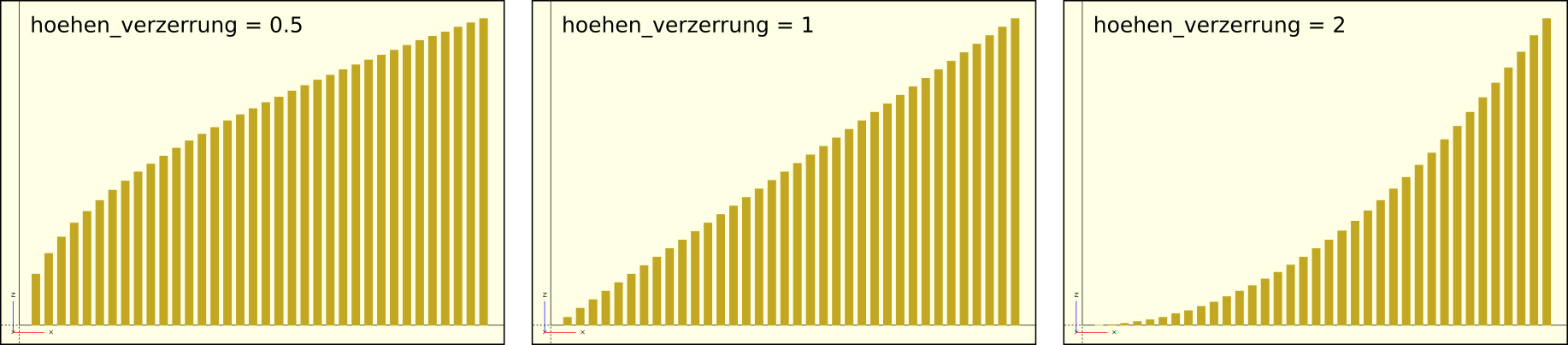
/* ... */Der Parameter hoehe gibt die Höhe des Pfades an, den wir erstellen wollen. Der Parameter ebenen gibt die Anzahl der Schritte an, die wir entlang es Pfades berechnen wollen. Hieraus können wir eine schrittweite ermitteln, die wir im weiteren Verlauf als interne Variable benötigen. Analog können wir eine Rotationsschrittweite rot_sw bilden. Die Positionen entlang unseres Pfades speichern wir als dreidimensionale Vektoren innerhalb eines Feldes. Wir berechnen die Positionen mit einer generativen For-Schleife. Die X- und Y-Koordinaten bewegen sich hierbei auf einer elliptischen Kreisbahn mit den Radien x_radius und y_radius, die sich schrittweise nach oben bewegt. Anstatt die Z-Koordinate linear anwachsen zu lassen, verwenden wir eine Potenzfunktion, um die Verteilung der Punkte entlang der Z-Achse mit dem Parameter hoehen_verzerrung beeinflussen zu können. Abbildung 9. gibt einen Eindruck davon, wie sich die Potenzfunktion für verschiedene Werte des Parameters hoehen_verzerrung verhält.
Neben der Positionierung möchten wir unsere Grundform entlang des Pfades auch skalieren. Dies soll nicht linear, sondern mit einer Sigmoid-Funktion geschehen. Da OpenSCAD keine “fertige” Sigmoid-Funktion anbietet, müssen wir uns diese selbst erstellen:
module flammen(
hoehe,
skalierung_start = [1.0, 1.0, 1.0],
skalierung_end = [0.1, 0.1, 0.1],
x_radius = 15,
y_radius = 10,
steilheit = 0.2,
uebergang = 0.35,
hoehen_verzerrung = 0.7,
rotationen = 1,
ebenen = 30
) {
// Positionen entlang des Pfades
/* ... */
// Skalierung entlang des Pfades
function sigmoid(x, steilheit = 0.5, uebergang = 0.5) =
let (
schrittweite = 1.0 - pow( steilheit, 0.1),
startpunkt = -uebergang / schrittweite
) 1 / ( 1 + exp( -( x / schrittweite + startpunkt) ) );
sk_faktor = [ for (i = [0:ebenen])
1.0 - sigmoid( i / ebenen, steilheit, uebergang )
];
}
/* ... */Wir definieren unsere Sigmoid-Funktion mittels der Exponentialfunktion exp und dem bekannten Schema 1 / (1 + exp(-x) ). Zusätzlich haben wir unsere Funktion so parametrisiert, dass der sigmoide Übergang im Intervall 0 bis 1 für den Parameter x liegt und wir die relative Position und Steilheit des sigmoiden Übergangs mittels der Parameter steilheit und uebergang einstellen können. Auch diese beiden Parameter erwarten Werte zwischen 0 und 1. Abbildung 9. gibt einen Eindruck davon, welche Wirkung verschiedene Werte für steilheit und uebergang auf die Ausgabe der Funktion haben.
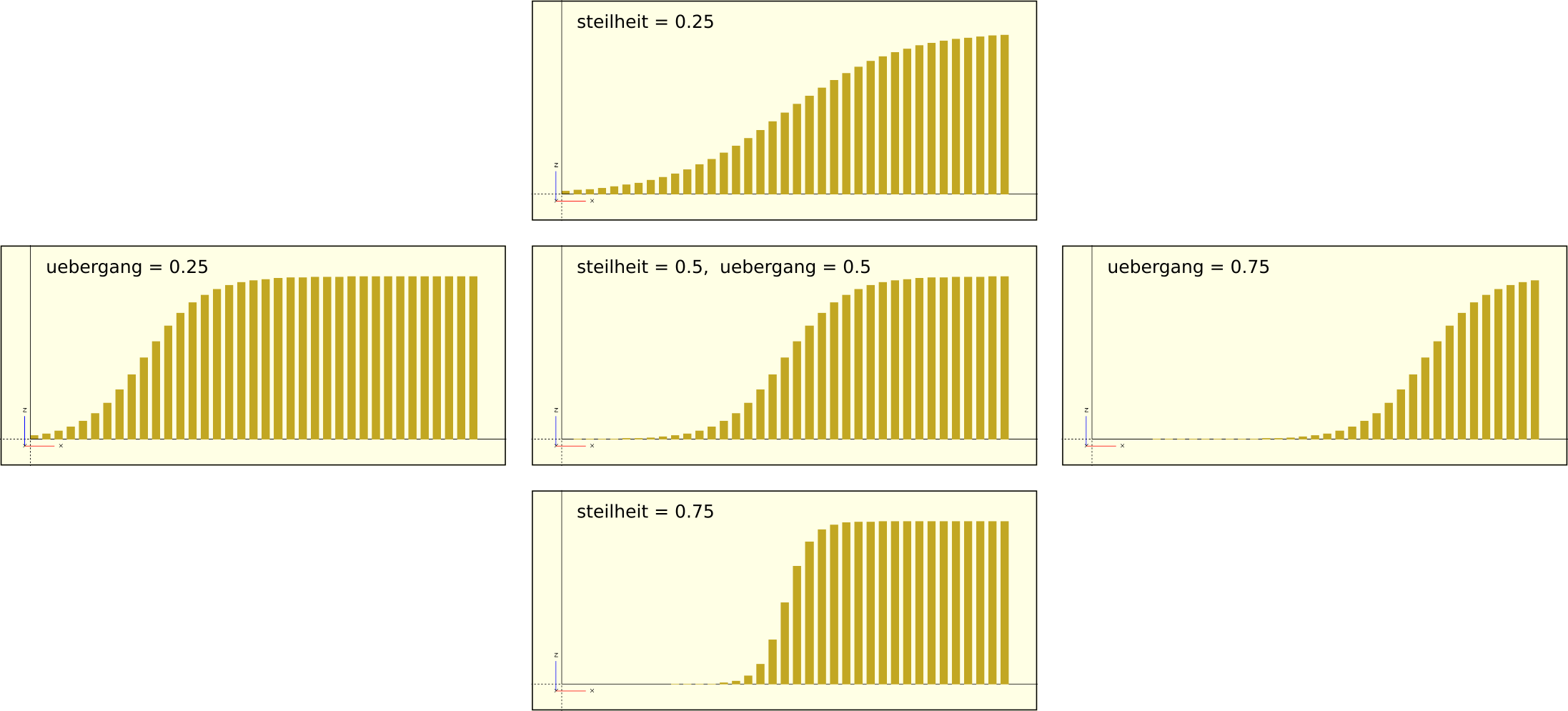
Wie auch die Positionen berechnen wir die Skalierungsfaktoren über eine generative For-Schleife und speichern sie im Feld sk_faktor ab. Bevor wir fortfahren, sollten wir schonmal eine provisorische Version einer einzelnen Flamme definieren, um zu sehen, ob wir auf dem richtigen Weg sind:
module flammen(
/* ... */
skalierung_start = [1.0, 1.0, 1.0],
skalierung_end = [0.1, 0.1, 0.1],
/* ... */
) {
// Positionen entlang des Pfades
/* ... */
// Skalierung entlang des Pfades
/* ... */
// Modul für eine einzelne Flamme
module flamme() {
for (i = [0:ebenen])
translate( positionen[i] )
linear_extrude( height = 2 )
scale(
skalierung_start * sk_faktor[i] +
skalierung_end * (1.0 - sk_faktor[i])
)
children(0);
}
flamme() children(0); // debug
}
flammen( 180 ) {
circle( d = 60 , $fn = 30);
sphere( d = 60 );
}Wir definieren ein Untermodul flamme und gehen innerhalb dieses Moduls mit einer For-Schleife parallel durch das positionen-Feld und das sk_faktor-Feld und nutzen ihre Werte, um eine 2D-Geometrie zu skalieren (scale) und zu verschieben (translate). Den Skalierungsvektor erzeugen wir als lineare Interpolation zwischen dem Vektor skalierung_start und dem Vektor skalierung_end, wobei der Interpolationswert aus dem Feld sk_faktor entnommen wird.
Zwischen Skalierung und Verschiebung führen wir eine lineare Extrusion aus, um die 2D-Geometrie in eine 3D-Geometrie zu überführen. Als 2D-Geometrie verwenden wir children(0), also das einer Instanz des Moduls flamme nachfolgende Element. Unterhalb unserer Moduldefinition des Moduls flamme haben wir testweise eine Instanz des Moduls instanziiert. Als nachfolgendes Element haben wir hier wieder children(0) verwendet! Dieses children(0) bezieht sich nun wiederum auf das nachfolgende Element des Moduls flammen (Plural!). Schauen wir bei dessen Instanz nach, so sehen wir, dass hier das erste nachfolgende Element ein Kreis (circle) mit Durchmesser 60 ist. Mit dieser Kette haben wir dieses äußere Element bis tief in ein Untermodul weitergeleitet.
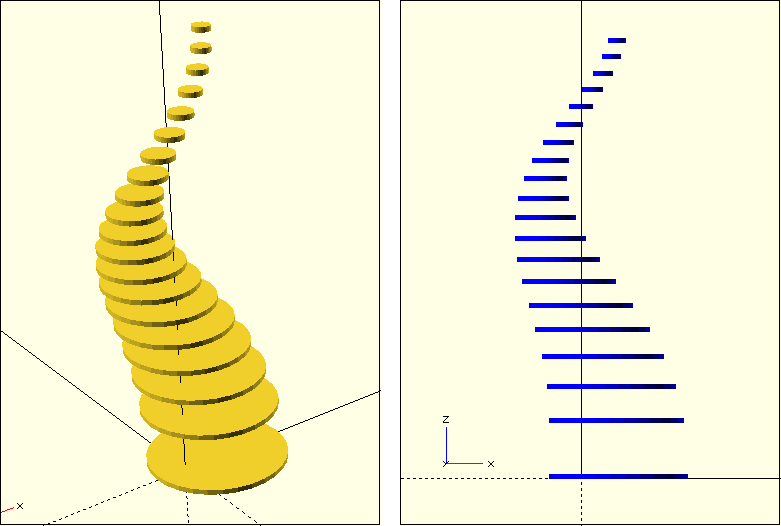
Abbildung 9. zeigt unseren bisherigen Zwischenstand. Die Kreisgeometrie folgt erkennbar einem geschwungenen Pfad und wird dabei skaliert. Rein theoretisch könnten wir jetzt die Kreise mittels der hull-Transformation paarweise verbinden und würden damit eine bereits recht passable 3D-Geometrie erhalten. Schöner wäre es jedoch, wenn sich die Kreise gemäß des Pfades neigen würden. Hierzu müssen wir herausbekommen, in welche Richtung der Pfad an der jeweiligen Stelle zeigt und dann den Kreis passend rotieren. Hierfür brauchen wir ein wenig Mathematik.
Den Cosinus des Winkels zwischen zwei Vektoren bekommen wir, wenn wir das Skalarprodukt der zwei Vektoren durch das Produkt der Längen der beiden Vektoren teilen. Für die Berechnung der Länge eines Vektors bietet OpenSCAD die Funktion norm an. Die Berechnung des Skalarprodukts müssen wir selbst definieren. Das Skalarprodukt zweier Vektoren v1 und v2 berechnet man, indem man die einzelnen Komponenten der Vektoren miteinander multipliziert und diese Produkte dann aufsummiert (v1[0] * v2[0] + v1[1] * v2[1] + ... + v1[n] * v2[n]). In den meisten Programmiersprachen würden wir hierfür elementweise durch die Vektoren gehen und nach und nach unsere Summe bilden. So eine “laufende Summe” können wir in OpenSCAD nicht bilden, da Variablen ja nur einmal ein Wert zugewiesen werden kann. Ausweg bietet hier die Verwendung von Rekursion:
module flammen(
/* ... */
) {
// Positionen entlang des Pfades
/* ... */
// Skalierung entlang des Pfades
/* ... */
// Winkel entlang des Pfades
function skalar_p(v1, v2, idx) = (
v1[idx] * v2[idx] +
(
idx > 0 ?
skalar_p(v1, v2, idx - 1) :
0
)
);
function skalarprodukt(v1, v2) = skalar_p(v1, v2, len(v1) - 1);
// Modul für eine einzelne Flamme
/* ... */
}
/* ... */
}Die Funktion skalar_p berechnet das Skalarprodukt zweier Vektoren v1 und v2 auf rekursive Weise. Hierfür hat die Funktion noch einen dritten Parameter idx. Die zweite Funktion skalarprodukt startet die Rekursion. Sie ruft skalar_p auf und setzt bei diesem initialen Aufruf den Wert des Parameters idx auf den Index des letzten Elementes (len(v1) - 1) der Vektoren. Die Funktion skalar_p berechnet daraufhin das Produkt der letzten Elemente von v1 und v2 und addiert abhängig vom Wert von idx entweder eine 0, oder den Wert, den der rekursive Aufruf der Funktion skalar_p ergibt. Der Trick - wie bei allen rekursiven Funktionen - besteht nun darin, dafür zu sorgen, dass die Funktion sich nicht unendlich oft selbst aufruft. Wir erreichen das an dieser Stelle dadurch, dass bei dem rekursiven Aufruf von skalar_p der Parameter idx den Wert idx - 1 bekommt. Der Wert von idx wird also mit jedem rekursiven Aufruf kleiner. Kommt er irgendwann bei 0 an, findet kein weiterer rekursiver Aufruf statt und die Funktion wird beendet. Auf dem Weg dahin haben wir die Produkte aller Elemente berechnet und aufsummiert. Als Endergebnis erhalten wir das gesuchte Skalarprodukt von v1 und v2. Falls Ihnen jetzt ein wenig der Kopf brummt: das ist eine ganz normale Nebenwirkung, wenn man sich mit rekursiven Algorithmen beschäftigt!
Nun können wir unser Skalarprodukt nutzen, um die Winkel entlang des Pfades zu berechnen:
module flammen(
/* ... */
) {
// Positionen entlang des Pfades
/* ... */
// Skalierung entlang des Pfades
/* ... */
// Winkel entlang des Pfades
/* ... */
function winkel(v1, v2) = acos( skalarprodukt(v1, v2) / ( norm(v1) * norm(v2) ) );
rel_pos = concat(
[ positionen[0] ],
[ for (i = [1:ebenen]) positionen[i] - positionen[i-1] ]
);
pos_winkel = concat(
[0],
[ for (i = [1:ebenen-1]) winkel( [0,0,1], rel_pos[i]) ],
[0]
);
// Modul für eine einzelne Flamme
/* ... */
}
/* ... */
}Wir definieren zunächst die Funktion winkel, die uns den Winkel zwischen zwei Vektoren v1 und v2 liefert. Wie zuvor beschrieben, teilen wir hierfür das Skalarprodukt durch das Produkt der Längen und ermitteln den Winkel über die Arkuscosinus-Funktion. Um die Winkel entlang des Pfades zu berechnen, müssen wir aus unseren absoluten positionen erst einmal die relativen Richtungen der einzelnen Pfadabschnitte bestimmen. Hierzu erzeugen wir ein Feld rel_pos das wir aus zwei Feldern mittels der Funktion concat zusammensetzen (engl. concatenate -> dt. konkatenieren bzw. aneinanderhängen). Das erste Feld enthält nur ein Element: die erste Position unseres Pfades. Das zweite Feld enthält für jede folgende Position des Pfades die Differenz zwischen dieser Position (positionen[i]) und der vorherigen Position (positionen[i-1]). Dementsprechend läuft die Schleifenvariable i auch nicht bei 0 sondern erst bei 1 los (i = [1:ebenen]). Insgesamt erhalten wir so ein Feld rel_pos dessen Einträge von 0 bis ebenen gehen. Es ist also genauso lang wie das Feld positionen.
Nun haben wir alle Vorbereitungen abgeschlossen, um endlich das Feld pos_winkel definieren zu können, welches die Winkel entlang des Pfades enthalten wird. Da wir für einen sauberen Abschluss die erste und die letzte 2D-Geometrie nicht drehen wollen, setzen wir das Feld pos_winkel aus drei einzelnen Feldern zusammen. Der erste und der letzte Eintrag wird hierbei einfach auf 0 gesetzt. Die Eintrage dazwischen erzeugen wir nun über eine generative For-Schleife, die unsere Funktion winkel nutzt, um den Winkel zwischen dem senkrechten Vektor [0, 0, 1] und dem jeweiligen relativen Pfadabschnitt rel_pos[i] zu berechnen. Auch hier haben wir darauf geachtet, dass die Einträge des Feldes pos_winkel von 0 bis ebenen gehen. Hierdurch wird die spätere Benutzung dieser Felder eleganter, da wir uns Fallunterscheidungen für den Anfang und das Ende des Pfades sparen können.
Jetzt können wir die Winkelinformation in unserem provisorischen Untermodul flamme zum Einsatz bringen:
module flammen(
/* ... */
) {
// Positionen entlang des Pfades
/* ... */
// Skalierung entlang des Pfades
/* ... */
// Winkel entlang des Pfades
/* ... */
// Modul für eine einzelne Flamme
module flamme() {
for (i = [0:ebenen])
translate( positionen[i] )
rotate( pos_winkel[i], cross([0,0,1], rel_pos[i]) )
linear_extrude( height = 2 )
scale(
skalierung_start * sk_faktor[i] +
skalierung_end * (1.0 - sk_faktor[i])
)
children(0);
}
flamme() children(0); // debug
}
/* ... */
}Wir fügen eine Rotationstransformation (rotate) vor der Verschiebung (translate) der Grundform ein. Wir nutzen hier die spezielle Variante der rotate-Transformation, der wir separat einen Winkel und einen Vektor übergeben können, um den die Drehung stattfinden soll. Als Winkel übergeben wir den zuvor ermittelten Winkel aus dem Feld pos_winkel. Die Drehachse ist der Vektor, der senkrecht auf dem Vektor unserer relativen Richtung rel_pos und der senkrechten im Ursprung des Koordinatensystems ([0, 0, 1]) steht. Dieser Vektor ergibt sich aus dem Kreuzprodukt der beiden anderen Vektoren. Glücklicherweise müssen wir das Kreuzprodukt nicht selber definieren, sondern können stattdessen die OpenSCAD-Funktion cross nutzen. Abbildung 9. zeigt, wie unser derzeitiger Zwischenstand aussieht.
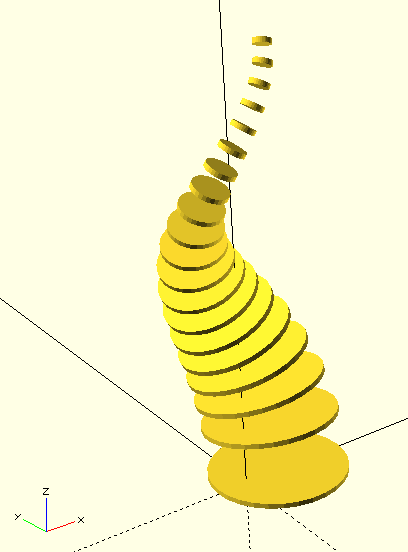
Im nächsten Schritt müssen wir das Untermodul flamme etwas umbauen. Unser Ziel ist es ja, die einzelnen Geometrien entlang des Pfades paarweise mit der hull-Transformation zu verbinden. Daher lösen wir die Geometriebeschreibung aus der For-Schleife heraus und verlagern sie in ein weiteres Untermodul ebene, dass wir mit der Schleifenvariable i indizieren können:
module flammen(
/* ... */
) {
// Positionen entlang des Pfades
/* ... */
// Skalierung entlang des Pfades
/* ... */
// Winkel entlang des Pfades
/* ... */
// Modul für eine einzelne Flamme
module flamme() {
module ebene( i ) {
translate( positionen[i] )
rotate( pos_winkel[i], cross([0,0,1], rel_pos[i]) )
linear_extrude( height = 0.01 )
scale(
skalierung_start * sk_faktor[i] +
skalierung_end * (1.0 - sk_faktor[i])
)
children(0);
}
for (i = [1:ebenen])
hull() {
ebene(i-1) children(0);
ebene(i) children(0);
}
}
flamme() children(0); // debug
}
/* ... */
}Das Untermodul ebene kapselt nun eine einzelne Grundform an der i-ten Position entlang des Pfades. Wir haben die zu Testzwecken auf 2 Millimeter gesetzte Extrusion nun auf 0.01 Millimeter reduziert. Damit arbeiten wir effektiv wieder mit 2D-Geometrien. Die For-Schleife im übergeordneten Modul flamme verbindet diese Ebenen paarweise. Man beachte, dass die Schleifenvariable i nun von 1 anstatt von 0 startet, damit wir in der Geometriemenge, die der hull-Transformation zugeführt wird, den Aufruf ebene(i-1) children(0); machen dürfen. Wie schon zuvor, müssen wir auch hier die von außen gesetzte Geometrie mittels children(0) in das Untermodul ebene herabreichen.

Damit ist die Geometriebeschreibung einer einzelnen Flamme vollständig (Abbildung 9.). Was jetzt noch bleibt, ist die Anordnung unserer einzelnen Flamme als Flammentripel. Vorher sollten wir nun die Testinstanz des Moduls flamme entfernen (// debug):
module flammen(
/* ... */
) {
// Positionen entlang des Pfades
/* ... */
// Skalierung entlang des Pfades
/* ... */
// Winkel entlang des Pfades
/* ... */
// Modul für eine einzelne Flamme
/* ... */
// Flammentripel
translate([-x_radius,0,0])
union(){
flamme()
children(0);
translate([x_radius,0,0])
rotate([0,0,120])
translate([-x_radius,0,0])
flamme()
children(0);
translate([x_radius,0,0])
rotate([0,0,240])
translate([-x_radius,0,0])
flamme()
children(0);
}
}
/* ... */
}Unser Flammentripel besteht im Wesentlichen aus einer Booleschen Vereinigung und drei Flammen, die jeweils um 120 Grad zueinander gedreht sind. Da die Grundformen innerhalb des Moduls flamme ihre geschwungene Kreisbahn immer bei [x_radius, 0] beginnen, müssen wir die Flammen vor der Rotation zeitweise in den Ursprung verschieben und nach der Rotation wieder zurück.
In seiner jetzigen Form endet das Flammentripel an seiner Spitze stumpf. Um die Situation zu verbessern, positionieren wir noch eine passend skalierte Kappe an die Spitze des Tripels. Die Geometrie hierfür lassen wir uns als zweites Element (children(1);) der externen Geometriemenge liefern:
module flammen(
/* ... */
) {
// Positionen entlang des Pfades
/* ... */
// Skalierung entlang des Pfades
/* ... */
// Winkel entlang des Pfades
/* ... */
// Modul für eine einzelne Flamme
/* ... */
// Flammentripel
/* ... */
// Kappe
if ($children > 1) {
translate([-x_radius,0,0])
translate(positionen[ebenen])
scale(
skalierung_start * sk_faktor[ebenen] +
skalierung_end * (1.0 - sk_faktor[ebenen])
)
children(1);
}
}
/* ... */
}Unsere Geometriebeschreibung ist nun vollständig! Durch den Ansatz, sowohl die 2D-Grundform als auch die Geometrie der abschließenden Kappe über eine externe Geometriemenge zu definieren, lässt sich unsere Flammenskulptur nun leicht anpassen. Darüber hinaus bieten die regulären Parameter des Moduls eine Reihe weiterer Einstellmöglichkeiten zur Feinabstimmung.
Abbildung 9. zeigt eine Reihe von Varianten, die nur durch Änderung der Ausgangsgeometrien und Parameter entstanden sind.

Hier sind die zugehörigen Instanziierungen der Varianten in Abbildung 9.:
// Nummer 1
flammen( 180 ) {
circle( d = 60 , $fn = 30);
sphere( d = 60 );
}
// Nummer 2
translate( [60, -60, 0] )
flammen(
180,
steilheit = 0.1,
uebergang = 0.3,
hoehen_verzerrung = 1.2,
ebenen = 30
) {
scale( [1, 0.33] )
circle( d = 60 , $fn = 30);
sphere( d = 120 );
}
// Nummer 3
union(){
translate( [125, -125, 0] )
flammen(
180,
skalierung_start = [1.0, 1.0, 1.0],
skalierung_end = [0.2, 0.2, 0.2],
steilheit = 0.3,
uebergang = 0.35,
hoehen_verzerrung = 0.5,
ebenen = 30
) {
square( 40, center = true);
cylinder( d1 = 50, d2 = 0, h = 30);
}
translate( [125, -125, 0] )
flammen(
180,
skalierung_start = [1.0, 1.0, 1.0],
skalierung_end = [0.2, 0.2, 0.2],
steilheit = 0.3,
uebergang = 0.35,
hoehen_verzerrung = 0.5,
ebenen = 30
) {
rotate( [0, 0, 45] )
square( 40, center = true);
cylinder( d1 = 50, d2 = 0, h = 30);
}
}
// Nummer 4
translate( [200, -200, 0] )
flammen(
180,
skalierung_start = [0.6, 0.6, 1.0],
skalierung_end = [0.4, 1.0, 1.0],
x_radius = 25,
y_radius = 15,
steilheit = 0.8,
uebergang = 0.6,
hoehen_verzerrung = 0.8,
rotationen = 1.3,
ebenen = 50
) {
square( [5, 45], center = true);
}