

Bei der Konstruktion technischer Bauteile kommt es regelmäßig vor, dass bereits existierende Komponenten integriert werden müssen. Im Kontext des 3D-Drucks sind dies häufig z.B. Motoren, Kugellager, Schrauben oder Muttern. In solchen Fällen ist es hilfreich, diese Komponenten auszumessen, nachzumodellieren und in der Geometriebeschreibung als Platzhalter zu verwenden. So kann man bereits im Computermodell sehen, ob alle Komponenten auch wirklich passen und am richtigen Ort sind. Wenn man bestimmte Bauteile häufiger verwendet, lohnt es sich, diese in einer OpenSCAD-Bibliothek abzulegen und dann mittels include bzw. use in das jeweilige Projekt einzubinden.
In diesem Projekt wollen wir uns genauer anschauen, was alles zu beachten ist, wenn wir eine nützliche OpenSCAD-Bibliothek erzeugen wollen. Als Übungsobjekt werden wir ein Standard-Uhrwerk nachmodellieren und die Geometriebeschreibung so gestalten, dass sie komfortabel als Teil einer OpenSCAD-Bibliothek genutzt werden kann.
Wir werden die 2D-Grundform import (dt. importieren) sowie die 3D-Grundform surface (dt. Oberfläche) kennenlernen. Als neue Transformationen werden wir mirror (dt. spiegeln) und resize (dt. Größe anpassen) nutzen. Darüber hinaus werden wir die Funktion search verwenden und etwas darüber erfahren, wie man mit OpenSCAD einfache Animationen erstellen kann.
Wir beginnen mit der Definition eines Moduls und beschreiben schonmal den quaderförmigen Grundkörper des Uhrwerks:
module uhrwerk() {
breite = 56;
tiefe = 56;
hoehe = 20;
// Grundkörper
color("Gray")
translate( [-breite / 2, -tiefe / 2, -hoehe] )
cube( [breite, tiefe, hoehe] );
}
uhrwerk(); // TestinstanzDa wir ein gegebenes, physisches Objekt nachmodellieren, können wir die gemessenen Größen als fest annehmen und brauchen sie daher nicht zu Parametern des Moduls zu machen. Anstelle dessen definieren wir sie als Variablen innerhalb des Moduls. Auch wenn unsere Geometriebeschreibung bislang wenig umfangreich ist, haben wir bereits eine wichtige Designentscheidung getroffen. Wir haben uns dazu entschlossen, den Grundkörper der Uhr so am Ursprung des Koordinatensystems auszurichten, dass die Oberfläche des Grundkörpers plan mit der X-Y-Ebene ist (Verschiebung entlang der Z-Achse um -hoehe) und dass später die Achse der Uhr mit der Z-Achse zusammenfällt (Verschiebung in X- und Y-Richtung um -breite / 2 und -tiefe / 2). Diese Ausrichtung wird nicht nur die folgenden Modellierungsschritte vereinfachen, sondern auch die Verwendung des Moduls uhrwerk als Teil einer OpenSCAD-Bibliothek.
Um die Achse des Uhrwerks ragt ein Ausrichtungsmuster aus dem Grundkörper hervor, dass aus einem abgeflachten, eingekerbten Zylinder besteht. Dieses Ausrichtungsmuster dient der Arretierung und Ausrichtung des Uhrwerks, wenn es in einer Uhr verbaut wird. Es ist also ein wichtiges Detail, das wir in unserer Geometriebeschreibung berücksichtigen sollten:
module uhrwerk() {
/* ... */
ausrichtung_dm = 14; // Durchmesser des Ausrichtungsmusters
ausrichtung_h = 1; // Höhe des Ausrichtungsmusters
ausrichtung_abfl = 1; // Rücksprung der Abflachungen
ausrichtung_kerbe_dm = 6; // Durchmesser der Kerben
ausrichtung_kerbe_tf = 2; // Rücksprung der Kerben
/* ... */
// Ausrichtungsmuster
difference(){
color("DimGray")
cylinder( d = ausrichtung_dm, h = ausrichtung_h, $fn = 36);
// Abflachung und Kerbe
color("Gray")
for ( i = [0:1])
mirror( [i, 0, 0] )
union(){
translate([
ausrichtung_dm / 2 - ausrichtung_abfl,
-(ausrichtung_dm + 2) / 2,
-1
])
cube([
ausrichtung_abfl + 1,
ausrichtung_dm + 2,
ausrichtung_h + 2
]);
translate([
ausrichtung_dm / 2 - ausrichtung_kerbe_tf +
ausrichtung_kerbe_dm / 2,
0,
-1
])
cylinder(
d = ausrichtung_kerbe_dm,
h = ausrichtung_h + 2,
$fn = 18
);
}
}
}
/* ... */Wir beschreiben das Ausrichtungsmuster über die Grundform Zylinder (cylinder), von der wir die Abflachung und Kerben mittels Boolescher Differenzoperation (difference) abziehen. Wir modellieren zunächst die Abflachung und Kerbe auf einer Seite des Hauptzylinders durch die Boolesche Vereinigung (union) eines Quaders (cube) und eines Zylinders (cylinder), die wir gemäß ihrer jeweiligen Rücksprünge passend zum Hauptzylinder positionieren. Da diese Objekte vom Hauptzylinder mittels difference abgezogen werden, achten wir bei der Dimensionierung (und Positionierung) auf ausreichende Zugaben, um eine saubere Differenzoperation zu gewährleisten.
Da unser Modell symmetrisch zum Ursprung ist, können wir Abflachung und Kerbe auf der anderen Seite des Hauptzylinders durch eine Kombination von Spiegeltransformation (mirror) und For-Schleife beschreiben. Der Parameter der Spiegeltransformation ist ein dreidimensionaler Vektor, der angibt, entlang welcher Achse wir unsere Geometrie spiegeln möchten. Ist der Vektor der Nullvektor ([0, 0, 0]), dann findet keine Spiegelung statt. Da unsere Schleifenvariable i genau einmal 0 und einmal 1 wird, erzeugen wir also sowohl unser ursprüngliches Abflachungs-Kerbe-Paar als auch das gespiegelte Paar auf der gegenüberliegenden Seite.
Wird das Uhrwerk in einer Uhr verbaut, wird es über eine zentrale Verschraubung befestigt. Potentielle Uhren müssen also an geeigneter Stelle ein passendes Loch aufweisen. Wir werden diese Verschraubungsachse nur als einfachen Zylinder modellieren und das feine Gewinde der Achse nicht in unser Modell aufnehmen:
module uhrwerk() {
/* ... */
verschraubung_dm = 7.8; // Durchmesser der Verschraubung
verschraubung_h = 5; // Höhe der Verschraubung gemessen vom Uhrwerk Grundkörper aus
/* ... */
// Verschraubung
color("Gold")
cylinder( d = verschraubung_dm, h = verschraubung_h, $fn = 36);
}
/* ... */Für die Geometrie des Uhrwerks fehlen nun nur noch die drei Achsen für die Stunden, Minuten und Sekundenzeiger:
module uhrwerk() {
/* ... */
stundenachse_dm = 5.1; // Durchmesser der Stundenachse
stundenachse_h = 8.3; // Höhe der Stundenachse
minutenachse_dm = 3.2; // Durchmesser der Minutenachse
minutenachse_h = 12.1; // Höhe der Minutenachse
sekundenachse_dm = 1; // Durchmesser der Sekundenachse
sekundenachse_h = 14.5; // Höhe der Sekundenachse
/* ... */
// Achsen
color("Black") {
cylinder( d = stundenachse_dm, h = stundenachse_h, $fn = 36);
cylinder( d = minutenachse_dm, h = minutenachse_h, $fn = 36);
cylinder( d = sekundenachse_dm, h = sekundenachse_h, $fn = 18);
}
}
/* ... */Wie auch die Verschraubung modellieren wir die Achsen als einfache Zylinder. Ein kleines Detail am Rande: die Verwendung der Farbtransformation (color("Black")) ist ein Beispiel dafür, dass Transformationen auch auf Geometriemengen ({ ... }) angewandt werden können.
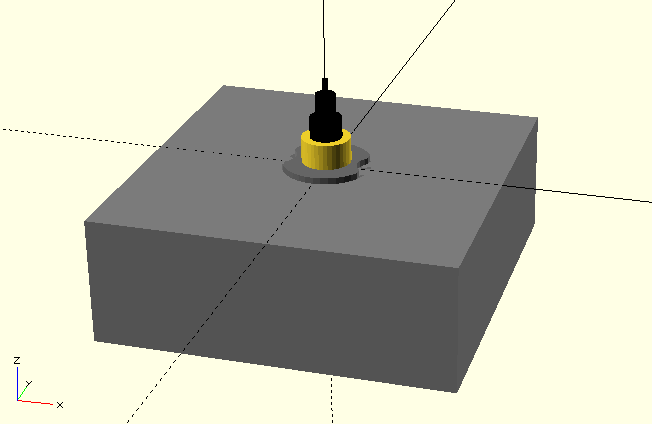
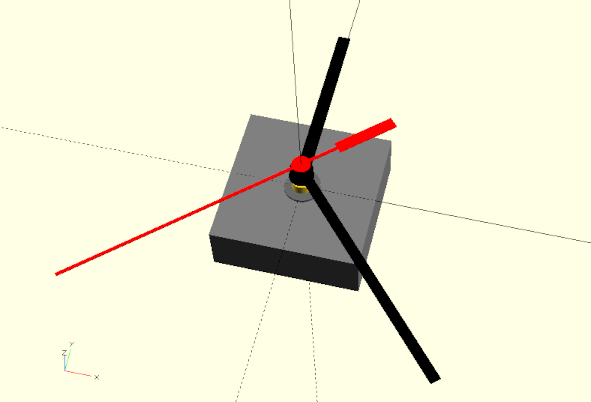
Unser nachmodelliertes Uhrwerk könnten wir schon jetzt als Platzhalter- und Kontrollobjekt bei der Konstruktion einer Uhr verwenden (Abbildung 6.). Für die Gestaltung einer Uhr wäre es jedoch deutlich angenehmer, wenn unser Modell auch einen Satz Zeiger hätte. Damit könnte man dann z.B. gleich sehen, ob das Ziffernblatt die richtigen Proportionen hat. Lassen Sie uns also unserem Uhrwerksmodell einen Satz Zeiger geben:
module uhrwerk( zeit = [12, 0, 0] ) {
/* ... */
// Zeiger
rotate( [0, 0, -360 * zeit[0] / 12] )
translate( [0, 0, stundenachse_h - 1] )
stundenzeiger();
rotate( [0, 0, -360 * zeit[1] / 60] )
translate( [0, 0, minutenachse_h - 1] )
minutenzeiger();
rotate( [0, 0, -360 * zeit[2] / 60] )
translate( [0, 0, sekundenachse_h ] )
sekundenzeiger();
module stundenzeiger( ) {
h = 0.4; // Höhe bzw. Materialstärke
l = 72.35; // Länge über alles
r = 67.6; // Radius (Drehpunkt zu Außenkante)
b = 5; // Breite
dm = 9.5; // Durchmesser Flansch
color("Black")
union() {
cylinder( d = dm, h = h, $fn = 36 );
translate( [-b / 2, 0, 0] )
cube( [b, r, h] );
}
}
module minutenzeiger() {
h = 0.4; // Höhe bzw. Materialstärke
l = 100.5; // Länge über alles
r = 96; // Radius (Drehpunkt zu Außenkante)
b = 4; // Breite
dm = 9; // Durchmesser Flansch
color("Black")
union() {
cylinder( d = dm, h = h, $fn = 36 );
translate( [-b / 2, 0, 0] )
cube( [b, r, h] );
}
}
module sekundenzeiger() {
b1 = 1.25; // Breite Vorderteil
l1 = 95; // Länge Vorderteil
b2 = 1.25; // Breite "Steg"
l2 = 15; // Länge "Steg"
b3 = 4.6; // Breite Hinterteil
l3 = 24; // Länge Hinterteil
dm = 7.1; // Durchmesser Flansch
h = 0.4; // Höhe bzw. Materialstärke
color("Red")
union() {
cylinder( d = dm, h = h, $fn = 36);
translate( [-b1 / 2, 0, 0] )
cube( [b1, l1, h] );
translate( [-b2 / 2, -l2, 0] )
cube( [b2, l2, h] );
translate( [-b3 / 2, -(l2 + l3), 0] )
cube( [b3, l3, h] );
}
}
}
/* ... */Wir haben unserem Modul uhrwerk einen Parameter zeit gegeben, der eine Testzeit als dreidimensionalen Vektor erwartet mit [Stunden, Minuten, Sekunden]. Für jeden Zeiger haben wir ein eigenes Untermodul definiert, so dass wir die jeweiligen Zeigergeometrien einfach auf die zugehörige Höhe verschieben und gemäß der Zeit um die Z-Achse drehen können. Hierbei rechnen wir die jeweiligen Zeitangaben in Winkelangaben um.
Die einzelnen Zeiger wurden ausgemessen, die Messwerte dann in Variablen innerhalb der Untermodule festgehalten und dort durch eine Kombination von 3D-Grundformen modelliert. Obwohl die Zeiger eine relativ einfache Form haben (Abbildung 6.1), ist dieses Vorgehen relativ aufwendig.

Da es durchaus üblich ist, dass einem Uhrwerk eine Auswahl verschiedener Zeigerstile beiliegt, ist die bisherige Vorgehensweise nicht besonders effektiv. Ein alternativer Weg besteht darin, die Zeiger in einem externen Zeichenprogramm zu zeichnen und als .svg-Datei abzuspeichern (Abbildung 6.). Mittels der import-Funktion von OpenSCAD können solche externen Zeichnungen dann als 2D-Grundform geladen werden:
module uhrwerk( zeit = [12, 0, 0], zeigerstil = "modern") {
/* ... */
module stundenzeiger() {
h = 0.4; // Höhe bzw. Materialstärke
l = 72.35; // Länge über alles
r = 67.6; // Radius (Drehpunkt zu Außenkante)
b = 5; // Breite
dm = 9.5; // Durchmesser Flansch
if (zeigerstil == "modern") {
/* ... */
}
if (zeigerstil == "deco") {
color("Black")
linear_extrude(height = h)
import("stunden.svg");
}
}
module minutenzeiger() {
h = 0.4; // Höhe bzw. Materialstärke
l = 100.5; // Länge über alles
r = 96; // Radius (Drehpunkt zu Außenkante)
b = 4; // Breite
dm = 9; // Durchmesser Flansch
if (zeigerstil == "modern") {
/* ... */
}
if (zeigerstil == "deco") {
color("Black")
linear_extrude(height = h)
import("minuten.svg");
}
}
module sekundenzeiger() {
b1 = 1.25; // Breite Vorderteil
l1 = 95; // Länge Vorderteil
b2 = 1.25; // Breite "Steg"
l2 = 15; // Länge "Steg"
b3 = 4.6; // Breite Hinterteil
l3 = 24; // Länge Hinterteil
dm = 7.1; // Durchmesser Flansch
h = 0.4; // Höhe bzw. Materialstärke
if (zeigerstil == "modern") {
/* ... */
}
if (zeigerstil == "deco") {
color("Black")
linear_extrude(height = h)
import("sekunden.svg");
}
}
}Das Modul uhrwerk hat einen weiteren Parameter zeigerstil bekommen, mit dem die Art der zu verwendenden Zeiger bestimmt werden kann. Innerhalb der Zeiger-Untermodule wird anhand des Stils eine Fallunterscheidung getroffen. Der Stil “modern” fügt der Geometriebeschreibung die per Hand modellierten und zuvor beschriebenen Zeiger hinzu. Beim Stil “deco” werden hingegen die Zeigerformen aus .svg-Dateien geladen und anschließend mittels linear_extrude in eine 3D-Geometrie umgewandelt. Die import-Funktion verhält sich hierbei wie jede andere 2D-Grundform und kann entsprechend auf gleiche Weise genutzt, z.B. transformiert, werden.

Die Nutzung des SVG-Imports für komplizierte 2D-Geometrien ist im Allgemeinen der beste Weg, derartige Geometrien in OpenSCAD zu nutzen. Es ist jedoch auch in hierfür spezialisierten Programmen wie z.B. Inkscape nicht ohne Aufwand, solche Geometrien zu erstellen. In unserem Anwendungsfall ist solch ein Aufwand nicht unbedingt gerechtfertigt, da wir die Zeiger in erster Linie als Anschauungsobjekt nutzen und bis auf ihre Gesamtmaße keinen Anspruch an Detailtreue haben. In solch einem Fall können wir Arbeitszeit durch Rechenzeit tauschen und uns die 2D-Geometrien direkt aus Fotos (Abbildung 6.) dieser Geometrien von OpenSCAD erstellen lassen. Die benötigte Rechenzeit und der benötigte Speicher sind dabei leider nicht zu unterschätzen und es kann passieren, dass der im Folgenden beschriebene Weg auf einem zu schwachen Computer nicht praktikabel ist. Zum Glück speichert OpenSCAD das Ergebnis dieser Rechnung zwischen, so dass sie nicht bei jeder Vorschau erneut durchlaufen werden muss!
Schauen wir uns an, wie wir aus .png-Bildern unsere Zeiger extrahieren können:
module uhrwerk( zeit = [12, 0, 0], zeigerstil = "modern") {
/* ... */
module stundenzeiger() {
/* ... */
if (zeigerstil == "modern") {
/* ... */
}
if (zeigerstil == "deco") {
/* ... */
}
if (zeigerstil == "klassisch") {
lk = 61;
color("Black")
png_zeiger( "stunden.png", lk, h, [-9.5, -6.75, 0]);
}
}
module minutenzeiger() {
/* ... */
if (zeigerstil == "modern") {
/* ... */
}
if (zeigerstil == "deco") {
/* ... */
}
if (zeigerstil == "klassisch") {
lk = 84;
color("Black")
png_zeiger("minuten.png", lk, h, [-9, -6.75, 0]);
}
}
module sekundenzeiger() {
/* ... */
if (zeigerstil == "modern") {
/* ... */
}
if (zeigerstil == "deco") {
/* ... */
}
if (zeigerstil == "klassisch") {
lk = 123;
color("Black")
png_zeiger("sekunden.png", lk, h, [-4,-36.8,0] );
}
}
module png_zeiger(dateiname, laenge, hoehe, null_verschiebung) {
translate( null_verschiebung )
linear_extrude( height = hoehe )
resize( [0, laenge], auto = true )
projection( cut = true )
translate( [0, 0, 75] )
surface( dateiname, invert = true );
}
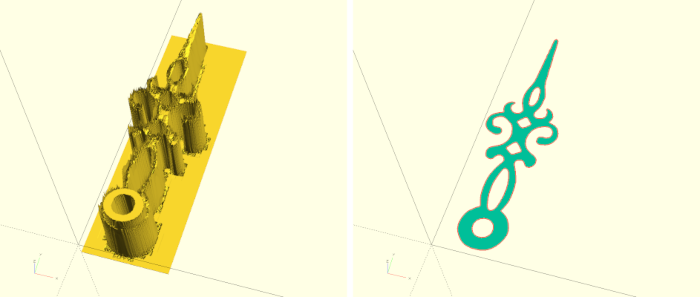
}Das neue Untermodul png_zeiger erzeugt einen Zeiger aus einer .png-Bilddatei. Zunächst nutzen wir die surface (dt. Oberfläche) Geometrie, um aus einer .png-Bilddatei ein Höhenrelief zu erzeugen. Normalerweise werden hierbei helle Farben als “hoch” und dunkle Farben als “niedrig” interpretiert. Durch den Parameter invert (dt. umkehren) wird diese Interpretation umgekehrt. Das so entstandene Höhenrelief verschieben wir nun derart nach oben, dass es die X-Y-Ebene an geeigneter Stelle schneidet (Abbildung 6. links). Wenden wir jetzt die projection-Transformation auf das Höhenrelief an, so schneiden wir das Relief genau in der X-Y-Ebene und erzeugen aus dem Schnitt eine hinreichend saubere 2D-Geometrie (Abbildung 6. rechts). Die so entstandene 2D-Geometrie hat leider nicht die passende Größe. Daher nutzen wir die resize-Transformation (dt. Größe anpassen), um die Geometrie auf eine gewünschte Länge zu skalieren. Die Breite lassen wir hierbei automatisch bestimmen und haben sie deshalb auf 0 gesetzt.
Im Anschluss können wir die nun korrekt skalierte 2D-Geometrie auf die gewünschte Höhe extrudieren und so verschieben, dass die Achse des Zeigers im Ursprung des Koordinatensystems liegt.
Um nicht bei jeder Nutzung des Uhrwerk-Moduls diese hohe Rechenzeit aufzuwenden, kann es sich lohnen, die Berechnung einmal durchzuführen und nach der resize-Operation die entstandene 2D-Form mit OpenSCAD als .svg-Datei zu speichern und diese dann wie oben beschrieben mittels import zu laden.
Im Prinzip ist unser Uhrwerk-Modul nun fertig und könnte in anderen Geometriebeschreibungen mittels use eingebunden und benutzt werden. Es gibt jedoch einen “Schönheitsfehler” an unserer bisherigen Vorgehensweise. Wenn Sie das Modul in einer anderen Geometriebeschreibung nutzen möchten, dann benötigen Sie fast zwangsläufig Informationen über die Maße des Uhrwerks. Diese stehen der anderen Geometriebeschreibung jedoch nicht zur Verfügung. Eine ad-hoc Lösung würde darin bestehen, die Datei des Uhrwerk-Moduls zu öffnen und die Werte händisch herausfinden. Eine etwas weniger unelegante Lösung würde darin bestehen, die derzeit innerhalb des Moduls uhrwerk definierten Variablen außerhalb des Moduls zu definieren. Wenn Sie dann die .scad-Datei mittels include anstelle von use einbinden, können Sie auf diese Variablen zugreifen. Es gibt jedoch zwei große Probleme mit dieser Lösung. Zum einen kann es zu Namenskollisionen kommen. Wir haben für das Uhrwerk zum Beispiel die Variablen breite, tiefe und hoehe definiert. Da ist die Wahrscheinlichkeit schon nicht gering, dass Sie diese Namen gerne auch in einem anderen Projekt verwenden würden. Schwieriger wird es gar, wenn sie in einer Bibliotheksdatei mehrere Module vorhalten wollen, die alle ihre eigenen Variablen benötigen. Man kann dieses Problem mit einer strikten Namenskonvention lösen. Schön ist das eher nicht. Das zweite große Problem besteht darin, dass Sie keine Kontrolle darüber haben, welche Variablen bzw. Informationen “exportiert” werden. Die Wahl zwischen include und use ist eine Wahl zwischen “alles” oder “nichts”. Wenn Sie sich für “alles” entscheiden, dann verlieren Sie die Möglichkeit, “lokale” Variablen außerhalb von Modulen zu definieren, die nur innerhalb ihrer Bibliothek gelten.
Eine bessere Lösung dieser Problematik kann wie folgt aussehen:
// Uhrwerk Konstanten
uhrwerk_daten = [
["breite", 56], // Breite des Grundkörpers
["tiefe", 56], // Tiefe des Grundkörpers
["höhe", 20], // Höhe des Grundkörpers
["ausrichtung_dm", 14], // Durchmesser des Ausrichtungsmusters
["ausrichtung_h", 1], // Höhe des Ausrichtungsmusters
["ausrichtung_abfl", 1], // Rücksprung der Abflachungen
["ausrichtung_kerbe_dm", 6], // Durchmesser der Kerben
["ausrichtung_kerbe_tf", 2], // Rücksprung der Kerben
["verschraubung_dm", 7.8], // Durchmesser der Verschraubung
["verschraubung_h", 5 ], // Höhe der Verschraubung
// gemessen vom Uhrwerk Grundkörper aus
["stundenachse_dm", 5.1], // Durchmesser der Stundenachse
["stundenachse_h", 8.3], // Höhe der Stundenachse
["minutenachse_dm", 3.2], // Durchmesser der Minutenachse
["minutenachse_h", 12.1], // Höhe der Minutenachse
["sekundenachse_dm", 1 ], // Durchmesser der Sekundenachse
["sekundenachse_h", 14.5] // Höhe der Sekundenachse
];
function uhrwerk_mass( name ) =
[ for (d = uhrwerk_daten) if (d[0] == name) d[1] ][0];Wir legen ein Feld mit Daten an, die wir zu unserer Geometrie nach außen zur Verfügung stellen wollen. In unserem Fall finden sich alle wichtigen Maße unseres Uhrwerks in dem Feld uhrwerk_daten. Um auf diese Daten zugreifen zu können auch wenn die Bibliothek mit use eingebunden wurde, müssen wir eine Funktion (hier: uhrwerk_mass) für den Zugriff bereitstellen. Diese Funktion bekommt als Parameter den Namen des Datenfeldes, dessen Daten wir auslesen möchten. Eine Möglichkeit, solch eine Funktion zu realisieren, ist die Nutzung einer generative for-Schleife. Wir laufen mit der Schleifenvariablen d durch das Feld uhrwerk_daten und fügen unserem Ergebnis-Feld genau dann ein Element (d[1]) hinzu, wenn der übergebene name dem Namen des Feldeintrags entspricht (if (d[0] == name)). Ergebnis dieser generativen For-Schleife ist ein Feld, dass nur einen Eintrag enthält: genau die Daten, die wir gerne aus uhrwerk_daten auslesen möchten. Was jetzt nur noch bleibt, ist auf diesen einen Eintrag des Feldes zuzugreifen. Dies macht das nachstehende [0].
Für kompliziertere Suchen über Daten stellt OpenSCAD den Befehl search zur Verfügung. Wie dieser genutzt werden kann, können wir am folgenden Beispiel sehen:
// Zeiger Konstanten
zeiger_daten = [
["stil", "modern", "klassisch", "deco"],
["stunden_l", 72.35, 61, 62.9], // Länge über alles
["stunden_r", 67.6, 56.6, 58.65], // Radius (Drehpunkt zu Außenkante)
["stunden_b", 5, 1.5, 2], // Breite an der Spitze
["stunden_h", 0.4, 0.4, 0.4], // Höhe bzw. Materialstärke
["minuten_l", 100.5, 84, 101.5], // Länge über alles
["minuten_r", 96, 79.5, 74.62], // Radius (Drehpunkt zu Außenkante)
["minuten_b", 4, 1, 1], // Breite an der Spitze
["minuten_h", 0.4, 0.4, 0.4], // Höhe bzw. Materialstärke
["sekunden_l", 134, 123, 120], // Länge über alles
["sekunden_r", 95, 88.4, 85.66], // Radius (Drehpunkt zu Außenkante)
["sekunden_b", 1.25, 0.6, 0.7], // Breite an der Spitze
["sekunden_h", 0.4, 0.4, 0.4] // Höhe bzw. Materialstärke
];
function zeiger_mass( name, stil ) =
let (
zeile = search( [name], zeiger_daten)[0],
spalte = search( [stil], zeiger_daten[0])[0]
) zeiger_daten[zeile][spalte];Hier haben wir alle Daten der verschiedenen Zeigervarianten zusammengefasst. Die Zugriffsfunktion zeiger_mass hat nun zwei Parameter. Einmal den Namen des Werts und einmal den Namen des Stils. Wir nutzen den Ausdruck let, um mittels search die Indizes der Zeile und Spalte herauszufinden, in der die angefragten Daten liegen. Auch hier taucht wieder die nachgestellte [0] auf, da search als Ergebnis ein Feld mit Indizes zurückliefert und wir nur am ersten Element dieses Feldes in diesem Fall interessiert sind. Der erste Parameter an search ist eine Liste bzw. ein Feld mit Suchbegriffen. Da wir nur nach jeweils einer Zeichenkette (name oder stil) suchen wollen, ist der erste Parameter ein Feld mit nur einem Eintrag. Der zweite Parameter ist das Feld, das durchsucht werden soll. Bei der Suche nach der richtigen Zeile möchten wir durch das komplette Feld zeiger_daten suchen. Hierbei schaut search standardmäßig nur den ersten Eintrag der Feldelemente an. Also hier genau die Namen der Datensätze. Für die Suche nach der richtigen Spalte durchsuchen wir nur den ersten Eintrag von zeiger_daten, der ja wiederum auch ein Feld ist. Auf diese Weise erhalten wir schließlich zwei Indizes zeile und spalte, mit der wir dann das gesuchte Datum aus dem Feld zeiger_daten auslesen und als Funktionswert zurückliefern können (zeiger_daten[zeile][spalte]).
Natürlich ist es sinnvoll, die Funktionen uhrwerk_mass und zeiger_mass auch innerhalb des Moduls uhrwerk für die Initialisierung der Variablen zu nutzen:
module uhrwerk( zeit = [12, 0, 0], zeigerstil = "modern") {
breite = uhrwerk_mass("breite");
tiefe = uhrwerk_mass("tiefe");
hoehe = uhrwerk_mass("höhe");
ausrichtung_dm = uhrwerk_mass("ausrichtung_dm");
ausrichtung_h = uhrwerk_mass("ausrichtung_h");
ausrichtung_abfl = uhrwerk_mass("ausrichtung_abfl");
ausrichtung_kerbe_dm = uhrwerk_mass("ausrichtung_kerbe_dm");
ausrichtung_kerbe_tf = uhrwerk_mass("ausrichtung_kerbe_tf");
verschraubung_dm = uhrwerk_mass("verschraubung_dm");
verschraubung_h = uhrwerk_mass("verschraubung_h");
stundenachse_dm = uhrwerk_mass("stundenachse_dm");
stundenachse_h = uhrwerk_mass("stundenachse_h");
minutenachse_dm = uhrwerk_mass("minutenachse_dm");
minutenachse_h = uhrwerk_mass("minutenachse_h");
sekundenachse_dm = uhrwerk_mass("sekundenachse_dm");
sekundenachse_h = uhrwerk_mass("sekundenachse_h");
/* ... */
module stundenzeiger() {
h = zeiger_mass("stunden_h",zeigerstil);
l = zeiger_mass("stunden_l",zeigerstil);
r = zeiger_mass("stunden_r",zeigerstil);
b = zeiger_mass("stunden_b",zeigerstil);
/* ... */
}
module minutenzeiger() {
h = zeiger_mass("minuten_h",zeigerstil);
l = zeiger_mass("minuten_l",zeigerstil);
r = zeiger_mass("minuten_r",zeigerstil);
b = zeiger_mass("minuten_b",zeigerstil);
/* ... */
}
module sekundenzeiger() {
h = zeiger_mass("sekunden_h",zeigerstil);
l = zeiger_mass("sekunden_l",zeigerstil);
r = zeiger_mass("sekunden_r",zeigerstil);
b = zeiger_mass("sekunden_b",zeigerstil);
/* ... */
}
/* ... */
}OpenSCAD bietet eine einfache Möglichkeit an, unsere Geometrien zu animieren und ggf. die Animationssequenz als Bildfolge abzuspeichern. Um unser Uhrwerk zu animieren, können wir unsere Geometriebeschreibung außerhalb des Moduls uhrwerk wie folgt erweitern:
/* ... */
function get_zeit( tick ) = [(tick / 3600) % 12, (tick / 60) % 60, tick % 60];
uhrwerk( get_zeit($t * 43200) , "modern");Wir definieren uns eine Funktion get_zeit, der wir als Parameter eine Sekundenzahl geben können und als Ergebnis einen dreidimensionalen Vektor mit Stunden, Minuten und Sekunden erhalten. Der %-Operator steht für den Modulo bzw. den Rest einer Division und sorgt dafür, dass die Minuten- und Sekundenwerte stets im Bereich 0 bis 59 liegen und dass der Stundenwert stets im Bereich 0 bis 11 liegt. Als Parameter übergeben wir der Funktion get_zeit nun den Ausdruck $t * 43200. Die Spezialvariable $t liefert die aktuelle Zeit innerhalb einer Animation zurück, wobei die Animationszeit als Fließkommazahl stets zwischen 0 und 1 verläuft. Wir skalieren also mit dem Ausdruck die Animationszeit auf den Bereich 0 bis 43200 (12 Stunden haben 43200 Sekunden).
Um nun die Animation zu starten, muss man das Animationsmenu sichtbar machen (View -> Animate). Dann erscheinen unter dem Anzeigefenster die drei Eingabefelder Time, FPS und Steps. Bei Steps tragen wir nun 43200 ein und bei FPS eine 1. Schon sollte sich unsere Uhr in Bewegung setzen und vor sich hin ticken. Man beendet die Animation, indem man das Animationsmenu wieder ausblendet (View -> Animate). Hakt man das Feld Dump Pictures an, dann wird jeder Animationsschritt zusätzlich als numerierte .png-Datei abgespeichert. Diese Dateien kann man im Anschluss nutzen, um sie z.B. in eine Video-Datei zu konvertieren. Unter Linux geht dies zum Beispiel mit dem Programm ffmpeg.