

Dieses Projekt hat die Konstruktion eines Fensterstoppers mit drehbarem Keil zum Ziel. Dreht man am Hebel des Stoppers, so verklemmt der Keil das Fenster mit der Fensterbank.

Wir lernen eine neue Variante der For-Schleife (generative for) kennen, mit der wir formelbasiert Felder erzeugen können. In diesem Zusammenhang werden wir auch die Bedeutung des Schlüsselwortes let kennenlernen und sehen, wie wir die erzeugten Daten mit der 2D-Grundform polygon in eine Geometrie überführen können. Zu guter Letzt werden wir auch erfahren, was es mit der Hüllentransformation (hull) auf sich hat.
Lassen Sie uns, wie inzwischen gewohnt, mit der Definition eines Moduls fensterstopper beginnen. Da wir auch bei diesem Projekt eine Menge Parameter erwarten, werden wir erneut ein senkrechtes Arrangement der Parameter wählen. Darüber hinaus wird unsere Geometriebeschreibung aus mehreren Teilen bestehen, die wir schonmal als Untermodule anlegen:
// Ein Fensterstopper mit drehbarem Keil
module fensterstopper(
/* parameter */
){
$fn = 36;
module fenster() {
}
module halter() {
}
module stopper() {
}
fenster();
halter();
stopper();
}
fensterstopper(
/* parameter */
);Auch wenn wir jedes Untermodul nur einmal nutzen werden, wird uns die Unterteilung in mehrere Untermodule helfen, wenn wir später die einzelnen Geometrieteile z.B. für einen 3D-Druck generieren wollen. Das Modul fenster wird ein reines Hilfsmodul, in dem wir die Unterkante des Fensters als Orientierungshilfe modellieren werden. Im Modul halter werden wir das Gehäuse des Fensterstoppers beschreiben und im Modul stopper werden wir den drehbaren Keil sowie seinen Hebel definieren. Neben den Untermodulen und ihren drei Instanzen haben wir auch die Spezialvariable $fn auf Modulebene definiert. Auf diese Weise können wir die Feinheit der runden Geometrien unserer Geometriebeschreibung an einer zentralen Stelle einstellen.
Beginnen wir unsere Geometriebeschreibung mit dem Hilfsmodul fenster:
/* ... */
module fensterstopper(
fenstertiefe, // Stärke des Fensters (inkl. Spiel) in Millimeter
fensterbank_abst, // Abstand zwischen Fensterbank und Unterkante Fenster in Millimeter
){
$fn = 36;
module fenster() {
color("LightSkyBlue")
translate( [-20, -fenstertiefe / 2, fensterbank_abst] )
cube( [100, fenstertiefe, 0.1] );
}
/* ... */
}
/* ... */Wir haben die Parameter fenstertiefe und fensterbank_abst unserem Modul hinzugefügt. Sie beschreiben die Dicke des Fensters und den Abstand der Unterkante des Fensters zur Fensterbank. Im Untermodul fenster beschreiben wir nur diese Unterkante des Fensters mit einem 0.1 Millimeter dünnen Quader (cube). Die Breite des Quaders setzen wir hier pauschal auf 10cm, da dieses Maß für die Konstruktion des Stoppers nicht relevant ist. Mittels der Verschiebetransformation (translate) bringen wir den Quader auf die Höhe fensterbank_abst und platzieren ihn in der Tiefe mittig über der X-Achse (-fenstertiefe / 2). Um unser Hilfsobjekt optisch vom Rest der Geometrie abzusetzen, geben wir ihm auch noch einen schönen Blauton. Da wir das Untermodul nur einmal verwenden und nicht parametrisieren müssen, ist die Parameterliste leer. Auf die Parameter des übergeordneten Moduls fensterstopper können wir direkt zugreifen und müssen diese nicht mittels lokaler Parameter “weiterreichen”. Dies gilt übrigens auch für Variablen, die im übergeordneten Modul definiert wurden. Dies werden wir uns im nächsten Schritt zunutze machen.
Die Geometriebeschreibung des Halters ist etwas aufwendiger. Im Kern besteht der Halter jedoch nur aus einem einfachen Quader (cube), von dem wir eine Reihe passend gedrehter und verschobener Grundformen (cube und cylinder) mittels einer Booleschen Differenzoperation (difference) abziehen:
/* ... */
module fensterstopper(
fenstertiefe, // Stärke des Fensters (inkl. Spiel) in Millimeter
fensterbank_abst, // Abstand zwischen Fensterbank und Unterkante Fenster
// in Millimeter
fensterbank_anp = 0, // Einfache Anpassung des Fensterbankabstands in Millimeter
halterbreite = 30, // Breite des Halters in Millimeter
materialstaerke = 5, // Materialstärke des Halters in Millimeter
fenster_ueberlappung = 7, // Überlappung von Halter und Fenster in Millimeter
achse_dm = 10, // Durchmesser der Drehachse in Millimeter
achse_spiel = 0.5, // Spiel der Drehachse in Millimeter
){
$fn = 36;
achshoehe = materialstaerke + (fensterbank_abst - materialstaerke) / 2;
/* ... */
module halter() {
halter_gr = [
halterbreite, // Breite
fenstertiefe + 2 * materialstaerke, // Tiefe
fensterbank_abst + fenster_ueberlappung // Höhe
];
translate( [0, -halter_gr.y / 2, 0] )
difference() {
cube( halter_gr );
translate( [-1, materialstaerke, materialstaerke] )
cube( [halter_gr.x + 2, fenstertiefe, halter_gr.z] );
achse_erw = achse_dm + achse_spiel;
translate( [halter_gr.x / 2, -1, achshoehe] )
rotate( [-90, 0, 0] )
cylinder( d = achse_erw, h = halter_gr.y + 2);
translate( [(halter_gr.x - achse_erw) / 2, -1, achshoehe] )
cube( [achse_erw, halter_gr.y + 2, halter_gr.z] );
}
translate( [0, -halter_gr.y / 2, -fensterbank_anp] )
cube( [halter_gr.x, halter_gr.y, fensterbank_anp] );
}
/* ... */
}
/* ... */Unsere Parameterliste hat reichlich Zuwachs bekommen. Der Parameter fensterbank_anp ermöglicht eine spätere Fein- bzw. Nachjustierung des Fensterstoppers. Die Parameter halterbreite und materialstaerke definieren die Breite des Halters und die Materialstärke der Seitenflächen und des Bodens des Halters. Mit dem Parameter fenster_ueberlappung legt man fest, wie weit der Halter seitlich mit dem Fenster überlappen soll. Die Parameter achse_dm und achse_spiel bestimmen den Durchmesser der Achse des drehbaren Keils sowie das Spaltmaß zwischen der Achse und ihrem Lager im Halter.
Innerhalb der Modulbeschreibung des Moduls fensterstopper definieren wir zunächst die Variable achshoehe, da wir diese nicht nur im Untermodul halter sondern auch später im Untermodul stopper benötigen werden. Wir positionieren die Achse auf halbem Weg zwischen Fensterbank und Unterkante des Fensters unter Berücksichtigung der Materialstärke des Halterbodens. Im Untermodul halter definieren wir eine weitere Variable halter_gr, die die Dimension unseres Halters in Abhängigkeit von Fenstermaßen, Materialstärke und Überlappung als dreidimensionalen Vektor beschreibt.
Die Geometrie des Halters beschreiben wir über eine Boolesche Differenzoperation (difference). Den Grundkörper, von dem wir die anderen Geometrien abziehen, bildet hier ein einfacher Quader, der die Außenmaße des Halters hat (cube( halter_gr );). Im Anschluss ziehen wir einen Quader ab, der eine zum Fenster korrespondierende Tiefe hat und etwas breiter ist, als unser Grundkörper (halter_gr.x + 2). Wir positionieren den Quader mittels Verschiebetransformation genau um die Materialstärke nach oben sowie um die Materialstärke nach innen. Hierdurch wird aus dem Grundkörper ein U-Profil, dass später entlang der Fensterkante verschoben werden kann. Beachten Sie auch die kleine Verschiebung in X-Richtung (-1), um eine saubere Differenzoperation zu gewährleisten.
Als nächstes müssen wir noch das Achslager von unserem Grundkörper abziehen. Da das Lager im Durchmesser etwas größer werden soll als die Achse selbst, definieren wir die Variable achse_erw als Summe von Achsdurchmesser und Achsspiel. Das Achslager besteht aus einem Zylinder (cylinder) und einem Quader (cube). Der Zylinder erhält den Durchmesser achse_erw und eine Höhe, die der Tiefe des Halters entspricht plus einer kleinen Zugabe. Da die Grundform cylinder senkrecht auf der X-Y-Ebene steht, müssen wir den Zylinder zunächst um die X-Achse auf die Seite drehen (rotate). Anschließend können wir den Zylinder mittels Verschiebetransformation (translate) auf die Mitte der Halterbreite (halter_gr.x / 2) und die eingangs berechnete achshoehe bewegen. Auch hier führen wir passend zur Zugabe in der Zylinderhöhe eine kleine Bewegung (-1) in Y-Richtung aus, um eine saubere Differenzoperation zu gewährleisten. Der zweite Teil des Achslagers besteht aus einem Quader, der genauso breit wie der Zylinder ist (achse_erw) und oberhalb der Achse aus der Haltergrundform geschnitten wird. Da die Grundform cube in diesem Fall ohne den Parameter center = true erstellt wurde, müssen wir bei der Verschiebung des Quaders in die Mitte des Halters seine eigene Breite berücksichtigen ((halter_gr.x - achse_erw) / 2). Davon abgesehen erfolgt die Positionierung des Quaders analog zu der des Zylinders zuvor. Auch hier achten wir wieder darauf, das die Differenzoperation sauber ablaufen kann (Zugabe in der Tiefe und korrespondierende Verschiebung).
Nachdem wir nun unseren kompletten Halter mit einer Booleschen Differenzoperation beschrieben haben, zentrieren wir den Halter noch über der X-Achse, indem wir der Differenzoperation (difference) eine entsprechende Verschiebung (translate) voranstellen.
Um den Abstand zwischen Fensterbank und Fenster auf eine zusätzliche, einfache Weise nachjustieren zu können, erstellen wir neben der Differenzoperation noch einen Sockel, der unterhalb des Halters bei Bedarf (Parameter fensterbank_anp) anwachsen kann. Dieser Sockel besteht aus einem einfachen Quader (cube), der die Grundfläche des Halters hat und fensterbank_anp hoch ist. Damit er “nach unten” anwächst, wird er mit einer Verschiebetransformation (translate) entsprechend um -fensterbank_anp entlang er Z-Achse verschoben. Mit der gleichen Transformation erledigen wir die Zentrierung des Sockels über der X-Achse (-halter_gr.y / 2);
Damit haben wir das Untermodul halter fertig und können uns nun endlich dem Untermodul stopper zuwenden. Da das Modul einige neue OpenSCAD-Funktionen verwendet, wollen wir hier schrittweise und etwas langsamer vorgehen:
/* ... */
module fensterstopper(
fenstertiefe, // Stärke des Fensters (inkl. Spiel) in Millimeter
fensterbank_abst, // Abstand zwischen Fensterbank und Unterkante Fenster
// in Millimeter
fensterbank_anp = 0, // Einfache Anpassung des Fensterbankabstands in Millimeter
halterbreite = 30, // Breite des Halters in Millimeter
materialstaerke = 5, // Materialstärke des Halters in Millimeter
fenster_ueberlappung = 7, // Überlappung von Halter und Fenster in Millimeter
achse_dm = 10, // Durchmesser der Drehachse in Millimeter
achse_spiel = 0.5, // Spiel der Drehachse in Millimeter
keil_start_r = 0, // Startradius des Keil in Millimeter
keil_end_r = 11, // Endradius des Keil in Millimeter
keil_winkel = 42, // Startwinkel des Keil in Grad
hebel_tiefe = 15, // Tiefe des Hebels in Millimeter
hebel_laenge = 40, // Länge des Hebels in Millimeter
hebel_winkel = 15, // Startwinkel des Hebels in Grad
){
$fn = 36;
achshoehe = materialstaerke + (fensterbank_abst - materialstaerke) / 2;
/* ... */
module stopper( winkel = 0 ) {
achse_laenge = fenstertiefe + 2 * materialstaerke + 2;
translate( [halterbreite / 2, -achse_laenge / 2, achshoehe] )
rotate( [-90, 0, 0] )
cylinder( d = achse_dm, h = achse_laenge, $fn = 36 );
/* ... */
}
/* ... */
}
/* ... */Für den Stopper haben wir einen weiteren Satz an Parametern definiert. Zum einen sind dies die drei Parameter keil_start_r, keil_end_r und keil_winkel, die wir später für die Beschreibung des Drehkeils benötigen. Zum anderen haben wir drei Parameter, die Eigenschaften des Stopperhebels definieren (hebel_tiefe, hebel_laenge, hebel_winkel). Wie schon im Modul halter werden wir auch in diesem Untermodul die Variable achshoehe nutzen. Darüber hinaus haben wir innerhalb des Untermoduls stopper die Variable achse_laenge definiert. Diese entspricht der Breite des Halters plus zwei Millimeter. Hierdurch wird die Achse jeweils einen Millimeter (vorne und hinten) aus dem Halter hervorstehen. Die Achse selbst wird über die Grundform cylinder modelliert und mittels Rotations- und Verschiebetransformation an die richtige Stelle bewegt. Das Untermodul stopper besitzt überdies einen Parameter winkel, den wir im weiteren Verlauf zum Testen der Funktion des Drehkeils verwenden werden.
Als nächstes werden wir den Drehkeil modellieren, der Teil der Achse wird. Für diesen Zweck werden wir zunächst mit einer speziellen Variante der For-Schleife ein Feld mit 2D-Punkten erzeugen, die den Drehkeil im Zweidimensionalen beschreiben. Anschließend übergeben wir diese Punktmenge an die 2D-Grundform Polygon (engl. ebenfalls polygon), die aus der Punktmenge eine nutzbaren 2D-Geometrie erzeugt. Diese können wir dann extrudieren und mit den gewohnten Rotations- und Verschiebetransformationen an den gewünschten Ort bewegen:
/* ... */
module fensterstopper(
/* ... */
){
$fn = 36;
achshoehe = materialstaerke + (fensterbank_abst - materialstaerke) / 2;
/* ... */
module stopper( winkel = 0 ) {
achse_laenge = fenstertiefe + 2 * materialstaerke + 2;
translate( [halterbreite / 2, -achse_laenge / 2, achshoehe] )
rotate( [-90, 0, 0] )
cylinder( d = achse_dm, h = achse_laenge, $fn = 36 );
points = [
for (i = [0:5:360])
let (radius = keil_start_r + (keil_end_r - keil_start_r) * i / 360 )
[ cos( i ) * radius, sin( i ) * radius ]
];
keilbreite = fenstertiefe - 2;
translate( [halterbreite / 2, -keilbreite / 2, achshoehe] )
rotate( [-90, 0, 0] )
rotate( [0, 0, keil_winkel + winkel] )
linear_extrude( height = keilbreite )
polygon(points);
/* ... */
}
/* ... */
}
/* ... */Das zentrale Element in der obigen Geometriebeschreibung ist die Variable points, der wir ein Feld zuweisen (points = [ ... ];). Ziel ist es, dieses Feld der 2D-Grundform polygon als Parameter zu übergeben. Die 2D-Grundform polygon erwartet ein Feld von 2D-Punkten bzw. zweidimensionalen Vektoren:
points = [ [x0,y0], [x1,y1], ..., [xN,yN] ];
polygon( points );Es ist leicht, bei all den eckigen Klammern etwas die Übersicht zu verlieren. Das “äußere” Feld besteht aus der eckigen Klammer ganz am Anfang und der ganz am Ende. Im Inneren befinden sich dann, durch Kommata getrennt, die einzelnen zweidimensionalen Vektoren mit ihren x- und y-Werten. Für einfache 2D-Formen könnte man also durchaus so eine Punktmenge per Hand definieren oder sie von einem externen Programm erzeugen lassen.
Für unseren Drehkeil gehen wir einen anderen Weg und nutzen eine generative For-Schleife (engl. generative for):
points = [
for (i = [0:5:360])
let (radius = keil_start_r + (keil_end_r - keil_start_r) * i / 360 )
[ cos( i ) * radius, sin( i ) * radius ]
];Die erste Zeile des Ausdrucks gleicht dem einer “normalen” For-Schleife. Wir definieren die Schleifenvariable i und weisen ihr eine Spanne zu, die von 0 in Schritten von 5 bis 360 läuft (for (i = [0:5:360])). Die nächste Zeile enthält etwas Neues. Der OpenSCAD Ausdruck let( ... ) erlaubt es, ein oder mehrere Variablen zu definieren, die in jedem Schleifendurchlauf neu gesetzt werden. Genau so, wie es auch mit der Schleifenvariable selbst geschieht. In unserem Fall definieren wir die Variable radius und geben ihr einen Wert, der sich im Laufe der Schleife stetig vergrößert. Auf diese Weise hat radius zu Beginn der Schleife den Wert keil_start_r und zum Ende der Schleife den Wert keil_end_r. In Worten lässt sich die Formel in etwa so beschreiben: wir starten mit keil_start_r und wollen am Ende bei keil_end_r landen. Der Unterschied bzw. der Abstand zwischen keil_end_r und keil_start_r ist (keil_end_r - keil_start_r). Um sich schrittweise dem Wert keil_end_r zu nähern, brauchen wir in jedem Schritt nur einen Bruchteil des Abstands (i / 360). Wenn i bei 360 angekommen ist, ist unser Bruchteil 360 / 360, also 1. Vorher ist i kleiner als 360 und ergibt damit einen Wert kleiner 1 für die jeweiligen Zwischenschritte.
Wir haben jetzt also eine Variable radius, die zunehmend größer wird. Wo kommen jetzt unsere Punkte her? Die finden wir in der dritten Zeile unserer generativen For-Schleife ([ cos( i ) * radius, sin( i ) * radius ]). Die dritte Zeile beschreibt die prototypische Form eines einzelnen Feldes. In unserem Fall ist dies erstmal ein zweidimensionaler Vektor ([ .. , .. ]). Der x-Wert des Vektors ist cos( i ) * radius und der y-Wert ist sin( i ) * radius. Hier verwenden wir also sowohl die Schleifenvariable i als auch die mit let definierte Variable radius. Für jeden Schritt der For-Schleife wird nun diese prototypische Form genommen, mit den jeweils aktuellen Werten ausgefüllt und dem Feld hinzugefügt. Wenn Sie sich das erzeugte Feld einmal anschauen wollen, dann können Sie (z.B.) unterhalb der Definition von points den OpenSCAD-Befehl echo( points ); einfügen und eine Vorschau (F5) berechnen lassen. Dann wird der Inhalt von points im Konsolenbereich von OpenSCAD ausgegeben.
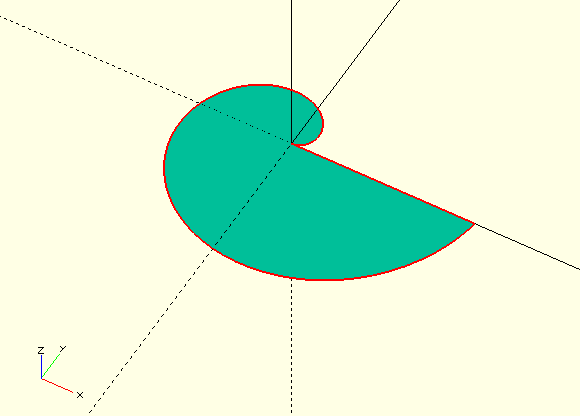
Übergibt man nun die Variable points als Parameter an die 2D-Grundform polygon, definiert die übergebene Punktmenge eine zweidimensionale Geometrie (Abbildung 5.). Diese Geometrie kann man dann wie jede andere zweidimensionale Grundform nutzen. Um unseren Drehkeil zu beschreiben, extrudieren wir die Form mittels linear_extrude auf die Länge keilbreite, die wir zuvor in Relation zur fenstertiefe definiert haben. Im Anschluss führen wir zunächst eine Rotation um die Z-Achse durch (rotate( [0, 0, keil_winkel + winkel] )). Diese Rotation erfüllt zwei Zwecke. Wir müssen zum einen sicherstellen, dass unser Keil nicht mit dem Halter kollidiert. Hierfür müssen wir einen geeigneten Wert für keil_winkel finden (Abbildung 5.). Ist einmal ein passender Wert gefunden, brauchen wir diesen nicht mehr zu verändern. Zum anderen nutzen wir die Rotation über den Parameter winkel zum späteren Testen der Funktionsfähigkeit unseres Drehkeils.
Anschließend führen wir eine zweite Rotation um die X-Achse aus, um den Drehkeil in die Waagrechte zu bekommen und ihn anschließend mittels einer Verschiebetransformation an die passende Stelle zu bewegen.
Nun können wir uns der Modellierung des Hebels als letzten Teil des Untermoduls stopper widmen. Hierbei werden wir die Hüllentransformation (engl. hull) kennenlernen:
/* ... */
module fensterstopper(
/* ... */
){
$fn = 36;
achshoehe = materialstaerke + (fensterbank_abst - materialstaerke) / 2;
/* ... */
module stopper( winkel = 0 ) {
achse_laenge = fenstertiefe + 2 * materialstaerke + 2;
translate( [halterbreite / 2, -achse_laenge / 2, achshoehe] )
rotate( [-90, 0, 0] )
cylinder( d = achse_dm, h = achse_laenge, $fn = 36 );
points = [
for (i = [0:5:360])
let (radius = keil_start_r + (keil_end_r - keil_start_r) * i / 360 )
[ cos( i ) * radius, sin( i ) * radius ]
];
keilbreite = fenstertiefe - 2;
translate( [halterbreite / 2, -keilbreite / 2, achshoehe] )
rotate( [-90, 0, 0] )
rotate( [0, 0, keil_winkel + winkel] )
linear_extrude( height = keilbreite )
polygon(points);
translate( [halterbreite / 2, -achse_laenge / 2 + 0.1, achshoehe] )
rotate( [0, hebel_winkel + winkel, 0] )
rotate( [90, 0, 0] )
linear_extrude( height = hebel_tiefe )
hull() {
circle( d = achse_dm );
translate( [hebel_laenge - achse_dm / 2 - achse_dm / 3, 0, 0] )
circle( d = achse_dm * 0.66 );
}
}
/* ... */
}
/* ... */Die Hüllentransformation (hull) wirkt ähnlich wie die Booleschen Operationen auf die jeweils nachfolgende Geometriemenge ({ ... }). Die Transformation erzeugt die gemeinsame konvexe Hülle der in dieser Menge enthaltenden Geometrien (Abbildung 5.). Die hull-Transformation kann sowohl auf 2D als auch auf 3D-Geometrien angewandt werden.
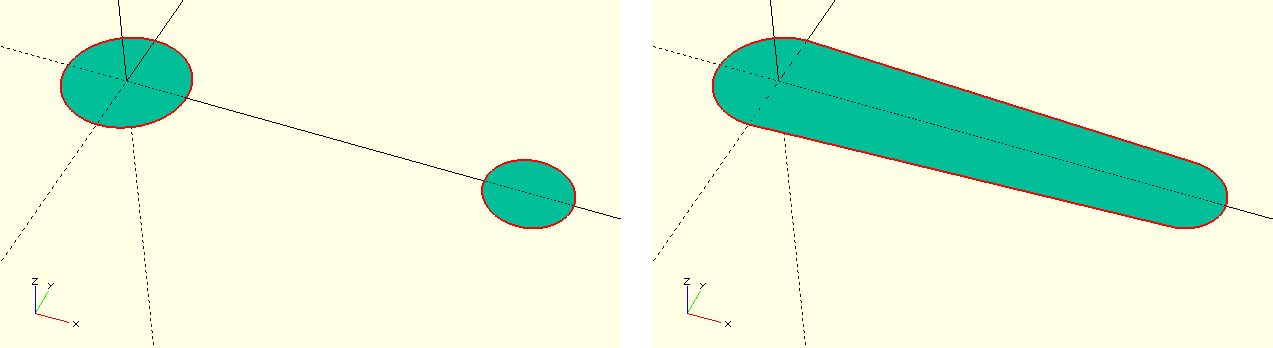
Für die Beschreibung des Hebels verwenden wir die 2D-Variante und bilden die konvexe Hülle über zwei Kreise (engl. circle). Die so entstehende Hebel-Grundform extrudieren wir mittels linear_extrude und drehen das Ganze um die X-Achse (rotate( [90, 0, 0] )). Stellt man der Rotationstransformation ein !-Zeichen voran und berechnet eine Vorschau (F5), so sieht man, dass die Y-Achse genau durch das Drehzentrum des Hebels verläuft. Wir können nun mit einer zweiten Rotationstransformation (rotate( [0, hebel_winkel + winkel, 0] )) den Hebel in seine Ausgangslage drehen, die durch den Parameter hebel_winkel bestimmt wird. Wie auch beim Drehkeil drehen wir zusätzlich um den Testparameter winkel. Auf diese Weise werden sich Drehkeil und Hebel gemeinsam drehen, wenn wir die Funktion des Stoppers über den Parameter winkel testen. Wir schließen die Geometriebeschreibung des Hebels ab, indem wir ihn mittels einer Verschiebetransformation (translate) an die passende Position bewegen. Man beachte die leichte Zugabe von 0.1 entlang der Y-Achse, um sicherzustellen, dass Hebel und Achse miteinander verbunden sind.
Wir haben es geschafft. Die Geometriebeschreibung für unseren Fensterstopper ist vollständig! An dieser Stelle sollten wir einmal testen, ob der Drehkeil sich auch tatsächlich unter das Fenster pressen wird. Dies können wir überprüfen, wenn wir Hebel und Drehkeil mit unserem Testparameter winkel des Stopper-Moduls einmal um 100 Grad gegen den Uhrzeigersinn drehen:
/* ... */
module fensterstopper(
/* ... */
){
/* ... */
fenster();
halter();
stopper( -100 );
}
/* ... */Wenn alles richtig gelaufen ist, sollte nun nach der Berechnung einer Vorschau (F5) der Drehkeil durch den blauen Quader der Fensterunterkante hindurchdringen.
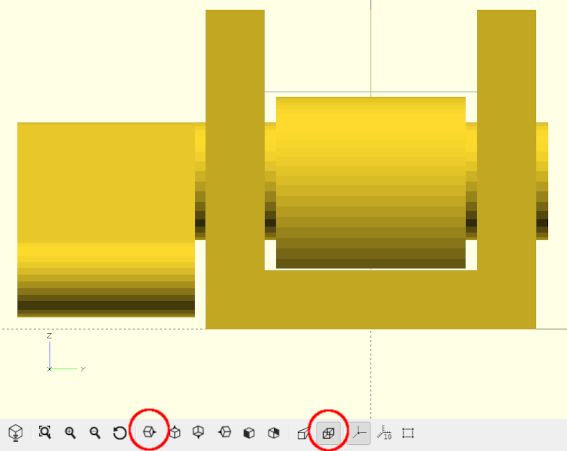
Um unseren Fensterstopper zu drucken, müssen wir die Untermodule halter und stopper getrennt voneinander berechnen lassen. Der einfachste Weg hierfür ist das zeitweise Voranstellen eines !-Zeichens vor der jeweiligen Modulinstanz. Löst man dann eine Geometrieberechnung aus (F6), kann man anschließend die so erzeugte Einzelgeometrie als .stl-Datei exportieren (F7).
Alternativ kann man das Modul fensterstopper noch um einen Parameter print_version erweitern und mittels Fallunterscheidung eine Positionierung der Module halter und stopper erzeugen, die den gleichzeitigen Export erlaubt:
/* ... */
module fensterstopper(
/* ... */
print_version = false
){
/* ... */
if (print_version) {
halter();
translate([
halterbreite,
0,
(fenstertiefe + 2 * materialstaerke + 2) / 2 + hebel_tiefe - 0.1
])
rotate( [90, 0, 0] )
stopper();
} else {
fenster();
halter();
stopper();
}
}
/* ... */In diesem Fall rotieren wir das Modul stopper in eine geeignete Druckausrichtung und verschieben es so, dass die Fußpunkte von halter und stopper in Z-Richtung gleich sind und sich insgesamt die Geometrien nicht überschneiden (Abbildung 5.).
