

Wenn Sie in einem älteren Haus wohnen, kennen Sie vielleicht dieses Problem. Sie möchten etwas an Wand oder Decke aufhängen, beginnen ein Loch zu bohren und plötzlich fängt der Bohrer an zu wandern. Am Ende haben Sie ein ziemlich großes Loch in der Wand, dass für die Schrauben, die Sie verwenden wollen, viel zu groß ist. In diesem Projekt wollen wir einen Spezialdübel entwerfen, der Ihnen in diesem Fall helfen kann.
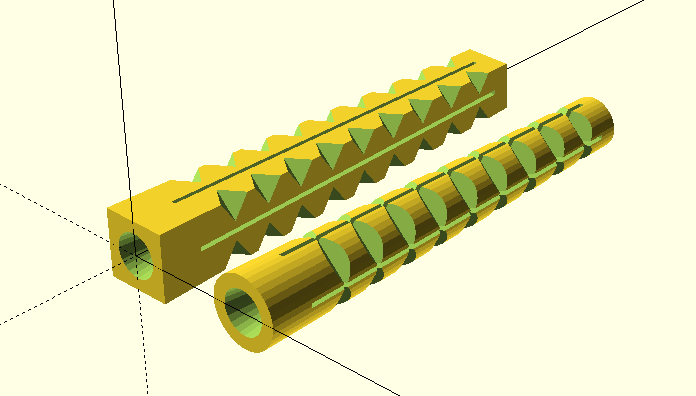
Wir werden unser erstes Extrusionsobjekt erstellen und dazu die 2D-Grundformen Quadrat (engl. square) und Kreis (engl. circle) sowie die lineare Extrusionstransformation linear_extrude verwenden. Darüber hinaus werden wir neue Varianten der Rotationstransformation rotate und der 3D-Grundform cylinder kennenlernen und unser Wissen über bereits bekannte Prinzipien und Funktionen vertiefen.
Lassen Sie uns auch hier damit beginnen, erst einmal ein Modul und eine Testinstanz dieses Moduls zu definieren:
// Ein Spezialdübel mit vielen Einstellmöglichkeiten
module duebel (
bohrloch_dm, // Durchmesser des Bohrlochs in Millimeter
schraube_dm, // Durchmesser der Schraube in Millimeter
laenge // Länge des Dübels in Millimeter
){
}
duebel(8,5,50);Da wir unserem Modul noch eine ganze Reihe an Parametern hinzufügen werden, arrangieren wir die Parameter dieses Mal als vertikale Liste. Dies erlaubt es uns zudem, die Parameter an Ort und Stelle mit einem erläuternden Kommentar zu versehen. Lassen Sie uns zunächst einen Dübel mit kantigem Grundkörper modellieren. Die runde Version des Dübels werden wir erst gegen Ende des Projektes der Modellbeschreibung als Option hinzufügen. Wenn der Dübel einen quadratischen Querschnitt hat und er in ein rundes Bohrloch passen soll, dann muss die Diagonale des Quadrats dem Durchmesser des Bohrlochs entsprechen. Um nun vom Durchmesser des Bohrlochs auf die Seitenlänge des Quadrats zu schließen, kann uns wieder der alte Pythagoras helfen:
/* ... */
module duebel (
bohrloch_dm, // Durchmesser des Bohrlochs in Millimeter
schraube_dm, // Durchmesser der Schraube in Millimeter
laenge // Länge des Dübels in Millimeter
){
seitenlaenge = sqrt( pow(bohrloch_dm, 2) / 2 );
linear_extrude(height = laenge)
square( seitenlaenge, center = true );
}
/* ... */Wir wissen, dass laut Pythagoras a^2 + b^2 = c^2 im rechtwinkligen Dreieck gilt. In diesem Fall ist die lange Seite des Dreieck c gegeben und wir suchen die Länge der kleinen Seiten. Da unser Dreieck in einem Quadrat liegt, wissen wir schonmal, dass die kleinen Seiten gleich lang sind. Wir können also unsere Formel umschreiben zu a^2 + a^2 = c^2 bzw. 2 x a^2 = c^2. Wenn wir jetzt noch die 2 auf die andere Seite ziehen, sind wir schon fast am Ziel: a^2 = c^2 / 2. Um a herauszubekommen, müssen wir nur noch die Wurzel ziehen: a = sqrt( c^2 / 2 ). Geschafft!
Den eckigen Grundkörper des Dübels beschreiben wir diesmal nicht durch die 3D-Grundform cube sondern über sein zweidimensionales Gegenstück square, welches wir anschließend mit einer linearen Extrusion (linear_extrude) in die Länge ziehen. Welchen Vorteil diese Vorgehensweise hat, sehen wir im nächsten Schritt.
Wie eingangs erwähnt, soll unser Dübel auch in “schwierigen” Bohrlöchern funktionieren, die durch ein verrutschen des Bohrers größer geworden sind als geplant. Daher verändern wir nun die Grundform so, dass sie keilförmig wird. Hierzu erstellen wir zwei neue Parameter, die uns erlauben, unseren Dübel nach Bedarf anzupassen. Dies wäre zum einen der Parameter uebergroesse, der dem Bohrdurchmesser hinzugefügt wird und zum anderen der Parameter aussen_vj, der einen Verjüngungsfaktor angibt, mit dem der Dübel zum Ende hin dünner wird. Man könnte an dieser Stelle sich auch überlegen, einen “Zieldurchmesser” anzugeben. Dies hätte jedoch zur Folge, dass man diesen Durchmesser immer mit angeben muss, da er ja passend zum Bohrlochdurchmesser gewählt werden muss. Die Version mit dem Verjüngungsfaktor erlaubt, dem Parameter einen Standardwert zu geben, der sich implizit auf den Bohrdurchmesser bezieht und damit nur geändert werden muss, wenn dieser Standardwert zu keinem guten Ergebnis führt. In der folgenden Geometriebeschreibung wird nun sichtbar, warum wir die Kombination square + linear_extrude anstelle von cube gewählt haben:
/* ... */
module duebel (
bohrloch_dm, // Durchmesser des Bohrlochs in Millimeter
schraube_dm, // Durchmesser der Schraube in Millimeter
laenge, // Länge des Dübels in Millimeter
uebergroesse = 2, // Übergröße des Außendurchmessers
aussen_vj = 0.75, // Verjüngungsfaktor des Außendurchmessers
){
aussen_dm = bohrloch_dm + uebergroesse;
seitenlaenge = sqrt( pow(aussen_dm, 2) / 2 );
linear_extrude(height = laenge, scale = aussen_vj)
square( seitenlaenge, center = true );
}
/* ... */Die Transformation linear_extrude bietet einen weiteren Parameter scale an, mit dem man die zu extrudierende 2D-Geometrie entlang der Extrusion verkleinern bzw. vergrößern kann. Mit Hilfe dieses Parameters können wir also sehr einfach die gewünschte, nach hinten zulaufende Form des Dübels beschreiben. Der Parameter uebergroesse kommt bei der Berechnung der seitenlaenge zum Einsatz.
Der Hohlraum innerhalb unseres Dübels, in dem wir die Schraube einschrauben, hat die Form eines Trichters. Zu Beginn hat das Loch im Dübel den Durchmesser der Schraube. Dann verjüngt es sich, damit die Schraube die Seiten des Dübels auseinanderdrücken und gegen die Innenseiten des Bohrlochs pressen kann. Wir können diese Trichterform aus zwei Zylindern herstellen und mittels einer Booleschen Differenzoperation von unserem Grundkörper abziehen:
/* ... */
module duebel (
bohrloch_dm, // Durchmesser des Bohrlochs in Millimeter
schraube_dm, // Durchmesser der Schraube in Millimeter
laenge, // Länge des Dübels in Millimeter
uebergroesse = 2, // Übergröße des Außendurchmessers
aussen_vj = 0.75, // Verjüngungsfaktor des Außendurchmessers
schraube_vj = 0.2, // Verjüngungsfaktor des Innendurchmessers
schraube_vjend = 0.3, // Relatives Ende der Verjüngung entlang der Tiefe
){
difference() {
aussen_dm = bohrloch_dm + uebergroesse;
seitenlaenge = sqrt( pow(aussen_dm, 2) / 2 );
linear_extrude(height = laenge, scale = aussen_vj)
square( seitenlaenge, center = true );
// Loch in Trichterform
svj_ende = laenge * schraube_vjend;
vj_dm = schraube_dm * schraube_vj;
translate([0,0,-0.01])
union() {
$fn = 24;
cylinder( d1 = schraube_dm, d2 = vj_dm, h = svj_ende + 0.01);
translate( [0, 0, svj_ende] )
cylinder( d = vj_dm, h = laenge - svj_ende + 0.02 );
}
}
}
/* ... */Wir haben unserem Modul zwei weitere Parameter hinzugefügt. Der Parameter schraube_vj setzt den Verjüngungsfaktor des Innendurchmessers und bestimmt, wie dünn der Hals unserer Trichterform wird. Der Parameter schraube_vjend bestimmt die Position an der der Hals unserer Trichterform beginnt. Die Position wird relativ zur laenge des Dübels angegeben. Innerhalb der Modulbeschreibung haben wir die Definition unseres Dübel-Grundkörpers zum ersten Element einer Booleschen Differenzoperation (difference) gemacht. Als zweites Element, welches vom Grundkörper abgezogen werden soll, haben wir unsere Trichterform beschrieben. Für diese berechnen wir zunächst aus den relativen Parametern schraube_vj und schraube_vjend die zugehörigen Absolutwerte svj_ende und vj_dm. Im Anschluss beschreiben wir die Trichterform mittels zweier Zylinder (engl. cylinder). Beim ersten Zylinder kommt eine neue Form der Parametrisierung zum Einsatz. Anstelle des Durchmessers d geben wir zwei Durchmesser d1 und d2 an. Hierdurch wird der Zylinder als stumpfer Kegel erzeugt, der unten den Durchmesser d1 und oben den Durchmesser d2 hat. In unserem Fall beginnen wir mit dem Schraubendurchmesser schraube_dm und enden mit dem Durchmesser der Verjüngung vj_dm. Die Höhe entspricht dem ausgerechneten Ende der Verjüngung svj_ende plus einer minimalen Zugabe. Der zweite Zylinder wird wieder ganz regulär mit nur einem Durchmesser definiert und beschreibt den Hals unserer Trichterform mit Durchmesser vj_dm und der restlichen Länge des Dübels (laenge - svj_ende) plus ebenfalls einer Zugabe. Schließlich fassen wir beide Zylinder mit einer Booleschen Vereinigung (union) zusammen und verschieben die Trichterform minimal nach unten, damit die Differenzoperation mit dem Dübel-Grundkörper sauber abläuft. An dieser Stelle können wir noch auf ein weiteres Detail eingehen: innerhalb der Booleschen Vereinigung (union) steht an erster Stelle die Spezialvariable $fn, mit der wir die Feinheit unserer Geometrie steuern können. Da wir die Feinheit beider Zylinder erhöhen wollen, können wir die Variable $fn einfach innerhalb der lokalen Geometriemenge der Booleschen Operation setzen, anstatt sie für jeden Zylinder einzelnd als Parameter angeben zu müssen.

!-ZeichensDa unsere Trichterform der subtraktive Teil einer Differenzoperation ist, ist es etwas schwierig, die Form “blind” zu modellieren. Wenn wir nun der Trichterform ein Ausrufezeichen voranstellen (!translate( ... ) union() ...) und eine Vorschau berechnen lassen, dann wird nur die Trichterform gezeichnet und keine andere Geometrie (Abbildung 4.). Diese selektive Vorschau einzelner Geometrieteile nutzt man erfahrungsgemäß sehr häufig und ist neben der transparenten Darstellung durch Voranstellen eines #-Zeichens (Abbildung 4.) eine der am häufigsten genutzten Modellierungshilfen.
Unserem Dübel fehlt jetzt noch die Möglichkeit, sich aufzuspreizen, wenn eine Schraube in den Dübel gedreht wird. Hierzu schlitzen wir den Dübel auf allen vier Seiten mittels geeigneter Quader (engl. cube) ein:
/* ... */
module duebel (
bohrloch_dm, // Durchmesser des Bohrlochs in Millimeter
schraube_dm, // Durchmesser der Schraube in Millimeter
laenge, // Länge des Dübels in Millimeter
uebergroesse = 2, // Übergröße des Außendurchmessers
aussen_vj = 0.75, // Verjüngungsfaktor des Außendurchmessers
schraube_vj = 0.2, // Verjüngungsfaktor des Innendurchmessers
schraube_vjend = 0.3, // Relatives Ende der Verjüngung entlang der Tiefe
kragen = 0.1, // Relative Länge des ungeschlitzten Teils
schlitzstaerke = 0.5, // Stärke der Schlitze in Millimeter
abschluss = 2, // Stärke der Abschlusskappe in Millimenter
){
difference() {
aussen_dm = bohrloch_dm + uebergroesse;
seitenlaenge = sqrt( pow(aussen_dm, 2) / 2 );
/* ... */
// Schlitze
kragen_abs = laenge * kragen;
for (i = [0:1])
rotate( [0, 0, i * 90] )
translate([
-(seitenlaenge + 2) / 2,
-schlitzstaerke / 2,
kragen_abs
])
cube ([
seitenlaenge + 2,
schlitzstaerke,
laenge - abschluss - kragen_abs
]);
}
}
/* ... */Für die Modellierung der Schlitze haben wir drei weitere Parameter unserem Modell hinzugefügt. Der Parameter kragen definiert, wie lang der Abschnitt zu Beginn des Dübels sein soll, in dem es noch keine Schlitze gibt. Der Anteil wird relativ zur Gesamtlänge angegeben. Der Parameter schlitzstaerke bestimmt die Dicke der Schlitze in Millimeter. Der Parameter abschluss legt fest, wie viele Meter vor Ende des Dübels die Schlitze wieder enden sollen. Dies dient der Stabilisierung des Dübels, da anderenfalls die geschlitzten Seitenteile frühzeitig abbrechen könnten. Innerhalb der Modulbeschreibung werden die Schlitze über einen Quader (cube) modelliert.
Dieser wird mittels einer Verschiebetransformation (translate) auf den Ursprung der X/Y-Ebene in Höhe der absoluten Kragengröße kragen_abs verschoben und anschließend um die Z-Achse rotiert (rotate). Die Rotation wird durch eine For-Schleife parametrisiert, die von 0 bis 1 läuft und somit 2 Instanzen des Quaders erzeugt: einmal um 0 Grad und einmal um 90 Grad gedreht. Zur Kontrolle können Sie die so entstehenden Quader temporär sichtbar machen, indem Sie der For-Schleife ein #-Zeichen voranstellen und eine Vorschau berechnen (Abbildung 4.).
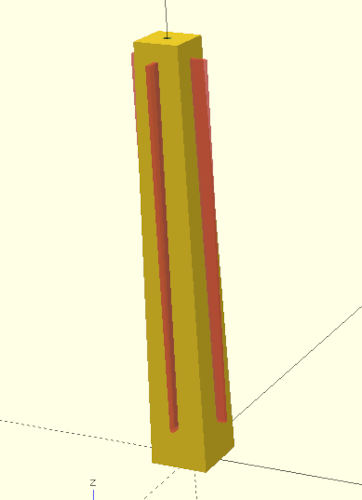
#-ZeichensUm sich in einem Bohrloch gut festkrallen zu können, wollen wir nun unserem Dübel noch ein paar Zähne verpassen:
/* ... */
module duebel (
bohrloch_dm, // Durchmesser des Bohrlochs in Millimeter
schraube_dm, // Durchmesser der Schraube in Millimeter
laenge, // Länge des Dübels in Millimeter
uebergroesse = 2, // Übergröße des Außendurchmessers
aussen_vj = 0.75, // Verjüngungsfaktor des Außendurchmessers
schraube_vj = 0.2, // Verjüngungsfaktor des Innendurchmessers
schraube_vjend = 0.3, // Relatives Ende der Verjüngung entlang der Tiefe
kragen = 0.1, // Relative Länge des ungeschlitzten Teils
schlitzstaerke = 0.5, // Stärke der Schlitze in Millimeter
abschluss = 2, // Stärke der Abschlusskappe in Millimenter
zahn_div = 5, // Divisor für die Anzahl der Zähne
zahn_tiefe = 1.5, // Tiefe der Zähne in Millimeter
){
difference() {
aussen_dm = bohrloch_dm + uebergroesse;
seitenlaenge = sqrt( pow(aussen_dm, 2) / 2 );
/* ... */
kragen_abs = laenge * kragen;
/* ... */
// Zähne
zahnanzahl = floor( (laenge - kragen_abs) / zahn_div );
zahnabstand = (laenge - kragen_abs) / (zahnanzahl + 1);
gegenkathete = (aussen_dm - (aussen_dm * aussen_vj)) / 2;
hypothenuse = sqrt( pow(gegenkathete, 2) + pow(laenge, 2) );
winkel = asin( gegenkathete / hypothenuse );
diag_abst = sqrt( pow(aussen_dm/2 - zahn_tiefe, 2) / 2 );
for ( j = [0:90:359])
rotate( [0, 0, j] )
rotate( -winkel, [1,1,0])
for ( i = [1:zahnanzahl] )
translate( [diag_abst, -diag_abst, kragen_abs + i * zahnabstand] )
rotate([0,0,-45])
translate( [0, -aussen_dm / 2, 0] )
rotate([0,45,0])
cube( aussen_dm );
}
}
/* ... */Für die Zähne definieren wir zwei weitere Parameter. Der Parameter zahn_div bestimmt die Anzahl der Zähne relativ zur Länge des Dübels. Der Parameter zahn_tiefe legt fest, wie tief die Zähne in den Grundkörper des Dübels eindringen sollen. Innerhalb der Modulbeschreibung generieren wir erst einmal aus dem Parameter zahn_div die absoluten Werte zahnanzahl und zahnabstand. Die bei der Zahnanzahl berücksichtigte Länge ist die Länge des Dübels abzüglich des Kragens. Die dort genutzte Funktion floor (dt. Fußboden) rundet den ihr übergebenen Wert ab, damit zahnanzahl ganzzahlig wird. Den Wert zahnabstand benötigen wir, um die Zähne gleichmäßig über den Dübel zu verteilen. Wir erhöhen hier die Zahnanzahl um 1, damit wir sowohl am Anfang als auch am Ende etwas Abstand zum Rand haben. Da unser Dübel-Grundkörper nach oben zuläuft, müssen wir noch den winkel der Seitenkante mit Hilfe des Arkussinus asin bestimmen. Und wir benötigen noch den Abstand diag_abst, der uns den Verschiebungswert in X- und Y-Richtung angibt, den man benötigt, um vom Ursprung an der äußeren Spitze der Dübelgrundfläche zu landen.
Nach diesen mathematischen Vorbereitungen können wir nun die Zahngeometrie beschreiben. Da unsere Geometriebeschreibung eine ganze Reihe von Schritten beinhaltet, ist es ratsam, sich jeden Schritt in der Vorschau anzuschauen, indem man an geeigneter Stelle ein !-Zeichen vor die Geometriebeschreibung setzt. Als Grundkörper wählen wir einen Würfel (cube) mit aussen_dm Kantenlänge. Setzen wir das !-Zeichen direkt vor cube und starten eine Vorschau (F5), dann wird nur dieser angezeigt. Im nächsten Schritt drehen wir den Würfel um 45 Grad entlang der Y-Achse (!rotate( [0, 45, 0] )). Dies erzeugt schon einmal die “Schneidfläche” entlang der Y-Achse, mit der wir später in den Grundkörper schneiden. Jetzt zentrieren wir den Würfel über der X-Achse indem wir ihn eine halbe Würfellänge entlang der Y-Achse verschieben (!translate( [0, -aussen_dm / 2, 0] )). Nun ist der Würfel in einer guten Position, um ihn um die senkrechte Z-Achse um -45 Grad zu drehen (!rotate([0,0,-45])). Jetzt steht der Würfel schon fast richtig. Wir müssen ihn nur noch auf die äußere Kante des Grundkörpers und etwas nach oben schieben (!translate( [diag_abst, -diag_abst, kragen_abs + i * zahnabstand] )). Bei dieser Verschiebung haben wir schon die Schleifenvariable i eingebaut. Wenn wir jetzt eine For-Schleife davor setzen, können wir uns einen Turm aus Würfeln bauen (!for ( i = [1:zahnanzahl] )).
Jetzt kommt der Punkt, wo wir uns um das Zulaufen unseres Dübel-Grundkörpers kümmern müssen. Unser Würfelturm soll ja der Seitenkante folgen, damit wir gleichmäßig unsere Zähne herausschneiden können. Hierzu kippen wir jetzt den Würfelturm um winkel. Da wir aber nicht um eine der Koordinatenachsen drehen wollen, sondern um eine Achse, die genau zwischen X- und Y-Achse liegt, benutzen wir an dieser Stelle eine besondere Form der Rotationstransformation rotate. Diese besondere Form bekommt als ersten Parameter den Winkel, um den man drehen möchte, und als zweiten Parameter die Achse, um die man drehen möchte (!rotate( -winkel, [1,1,0])).
Wir haben es fast geschafft! Jetzt müssen wir unseren gekippten Würfelturm nur noch dreimal kopieren und dabei jeweils um 90 Grad drehen. Dies erledigen wir mit einer zweiten For-Schleife und einer entsprechenden Rotationstransformation (!for ( j = [0:90:359]) rotate( [0, 0, j] )). Die For-Schleife endet bei 359 und nicht etwa bei 360, da wir ansonsten Würfeltürme bei 0 Grad und bei 360 Grad hätten, die übereinander lägen.
Als finalen “Touch” wollen wir unserem Spezialdübel noch die Option geben, anstelle eines viereckigen Grundkörpers auch einen runden Grundkörper zu haben:
module duebel (
bohrloch_dm, // Durchmesser des Bohrlochs in Millimeter
schraube_dm, // Durchmesser der Schraube in Millimeter
laenge, // Länge des Dübels in Millimeter
uebergroesse = 2, // Übergröße des Außendurchmessers
aussen_vj = 0.75, // Verjüngungsfaktor des Außendurchmessers
schraube_vj = 0.2, // Verjüngungsfaktor des Innendurchmessers
schraube_vjend = 0.3, // Relatives Ende der Verjüngung entlang der Tiefe
kragen = 0.1, // Relative Länge des ungeschlitzten Teils
schlitzstaerke = 0.5, // Stärke der Schlitze in Millimeter
abschluss = 2, // Stärke der Abschlusskappe in Millimenter
zahn_div = 5, // Divisor für die Anzahl der Zähne
zahn_tiefe = 1.5, // Tiefe der Zähne in Millimeter
rund = false // Erstelle runden anstatt eckigen Dübel
){
difference() {
aussen_dm = bohrloch_dm + uebergroesse;
seitenlaenge = rund ? aussen_dm : sqrt( pow(aussen_dm, 2) / 2 );
linear_extrude(height = laenge, scale = aussen_vj)
if (rund)
circle(d = seitenlaenge, $fn=36);
else
square( seitenlaenge, center = true );
// Loch
svj_ende = laenge * schraube_vjend;
vj_dm = schraube_dm * schraube_vj;
translate([0,0,-0.01])
union() {
$fn = 24;
cylinder( d1 = schraube_dm, d2 = vj_dm, h = svj_ende + 0.01);
translate( [0, 0, svj_ende] )
cylinder( d = vj_dm, h = laenge - svj_ende + 0.02 );
}
// Schlitze
kragen_abs = laenge * kragen;
for (i = [0:1])
rotate( [0, 0, i * 90] )
translate([
-(seitenlaenge + 2) / 2,
-schlitzstaerke / 2,
kragen_abs
])
cube ([
seitenlaenge + 2,
schlitzstaerke,
laenge - abschluss - kragen_abs
]);
// Zähne
zahnanzahl = floor( (laenge - kragen_abs) / zahn_div );
zahnabstand = (laenge - kragen_abs) / (zahnanzahl + 1);
gegenkathete = (aussen_dm - (aussen_dm * aussen_vj)) / 2;
hypothenuse = sqrt( pow(gegenkathete, 2) + pow(laenge, 2) );
winkel = asin( gegenkathete / hypothenuse );
diag_abst = sqrt( pow(aussen_dm/2 - zahn_tiefe, 2) / 2 );
for ( j = [0:90:359] )
rotate( [0, 0, j] )
rotate( -winkel, [1,1,0] )
for (i = [1:zahnanzahl] )
translate( [diag_abst, -diag_abst, kragen_abs + i * zahnabstand] )
rotate([0,0,-45])
translate( [0, -aussen_dm / 2, 0] )
rotate([0,45,0])
cube( aussen_dm );
}
}
duebel(8,5,50);Die Option den Dübel rund oder eckig zu gestalten wird über den neu hinzugefügten Parameter rund gesteuert. Innerhalb der Geometriebeschreibung haben wir zwei Stellen mit einer Fallunterscheidung erweitert. Zum einen wird die Seitenlänge in Abhängigkeit des Parameters rund gesetzt. Zum anderen wird mittels einer If-Verzweigung zwischen runder (circle) und eckiger (square) Grundform unterschieden. Man beachte, das hier die If-Verzweigung selbst wieder wie eine Geometrie behandelt wird, die von linear_extrude extrudiert wird.
Unser fertiges Dübel-Modul hat eine ganze Menge an Parametern erhalten! Dadurch, dass wir den großen Teil der Parameter jedoch als relative Parameter gestaltet haben und den Parametern sinnvolle Standardwerte gegeben haben, bleibt das Modul angenehm benutzbar. Im Regelfall müssen nur die drei Parameter bohrloch_dm, schraube_dm und laenge angegeben werden. Alles andere passt sich automatisch den Gegebenheiten an.
Nachdem Sie die Geometrie berechnet (F6) und anschließend als .stl-Datei exportiert (F7) haben, können Sie die .stl-Datei in die Slicer-Software ihres 3D-Druckers einladen. Hier stellt sich die Frage, ob Sie den Dübel stehend oder liegend drucken wollen. Liegend dürfte der Dübel etwas stabiler werden und weniger Druckzeit benötigen, dafür jedoch eine Stützstruktur benötigen, die Sie nach dem Druck entfernen müssen. Wenn Sie den Dübel stehend drucken, fällt die Notwendigkeit einer Stützstruktur weg. Hier sollten Sie ggf. die Druckgeschwindigkeit etwas verringern, damit die einzelnen Schichten genug Zeit haben, ausreichend abzukühlen, bevor die nächste Schicht aufgebracht wird. Darüber hinaus könnte es von Vorteil sein, mit einem sogenannten Brim zu drucken, damit sich die Standfläche des Dübels auf dem Druckbett vergrößert und somit die Druckbetthaftung verbessert wird.