

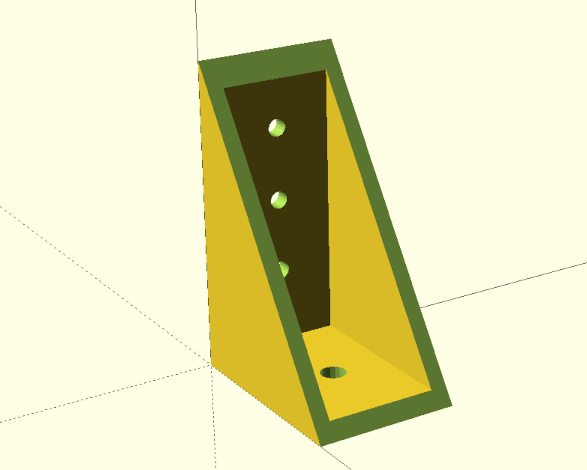
In diesem Projekt geht es darum, einen Regalbodenwinkel zu konstruieren. Hierbei sollen sowohl die Längen der beiden Schenkel als auch die Größe und Anzahl der Löcher frei einstellbar sein.
Wir werden die Boolesche Vereinigung (engl. union) als neue Boolesche Operation kennenlernen. Darüber hinaus werden wir ein paar mathematische Funktionen (Wurzel, Potenz und Arkuscosinus) von OpenSCAD nutzen sowie mehr über die Funktionsweise von Modulen erfahren. Zu guter Letzt werden wir uns die Projektionsfunktion (engl. projection) anschauen und sie dazu verwenden, uns Bohrschablonen für unseren Regalbodenwinkel zu erstellen.
Lassen Sie uns als erstes ein leeres Modul regalbodenwinkel erstellen und darüber nachdenken, welche Parameter wir benötigen. Wir wollen die Länge jeder Seite, sowie die Größe und Anzahl der Löcher verändern können. Darüber hinaus hat unser Winkel sicher auch eine Breite und wir müssen wissen, welche Materialstärke der Winkel haben soll. Das sind eine Menge Parameter! Damit unsere Parameterliste nicht allzu lang wird, können wir uns vornehmen die Werte jeder Seite (Länge, Lochdurchmesser, Anzahl der Löcher) in einem dreidimensionalen Vektor zusammenfassen:
/*
Modul Regalbodenwinkel
Parameter:
- seite_a ist ein Vektor [Länge, Lochdurchmesser, Anzahl Löcher]
- seite_b ist ein Vektor [Länge, Lochdurchmesser, Anzahl Löcher]
- breite ist die Breite des Winkels
- dicke ist die Materialstärke des Winkels
*/
module regalbodenwinkel( seite_a, seite_b, breite, dicke ) {
}
regalbodenwinkel(
seite_a = [50, 6, 1],
seite_b = [75, 4, 3],
breite = 35,
dicke = 4
);Über unserem Modul haben wir einen mehrzeiligen Kommentar (/* ... */) verfasst, der kurz erläutert, welche Parameter es gibt und welche Art von Eingaben diese Parameter erwarten. Auch wenn niemand anderes ihr Modul nutzen wird, ist ein solcher Kommentar sinnvoll. Wenn Sie in 6 Monaten nochmal einen Regalbodenwinkel brauchen, werden Sie sich über den hilfreichen Kommentar freuen! Unterhalb des Moduls regalbodenwinkel haben wir das Modul einmal mit konkreten Werten instanziiert. Ohne diese konkrete Instanz, würden wir bei der schrittweisen Entwicklung des Moduls keine Geometrie im Ausgabefenster sehen. Darüber hinaus können wir die Instanz nutzen, um während der Entwicklung immer mal wieder die Parameter zu verändern, um zu prüfen, ob sich unsere Geometriebeschreibung so verhält, wie von uns erwartet.
Wenn man den geplanten Regalbodenwinkel betrachtet (Abbildung 3.), dann fällt auf, dass die beiden Seiten des Winkels im Prinzip gleich sind. Sie bestehen aus einem Quader und gleichmäßig über die Mittelachse verteilten Löchern. Wir brauchen diese Geometrie für beide Seiten. Daher lohnt es sich, auch hierfür ein Modul zu schreiben. Da wir dieses Modul nur für den Winkel brauchen, definieren wir es innerhalb des Moduls regalbodenwinkel als Untermodul xloch_platte und verwenden anschließend das Untermodul für Seite A und Seite B des Winkels:
/* ... */
module regalbodenwinkel( seite_a, seite_b, breite, dicke ) {
module xloch_platte(groesse, l_dm, l_anz, randabstand) {
difference(){
cube(groesse);
lochabstand = (groesse.x - randabstand) / (l_anz + 1);
for (x = [1:l_anz])
translate ([
randabstand + x * lochabstand,
groesse.y/2,
-1
]) cylinder( d = l_dm, h = groesse.z + 2, $fn=18);
}
}
// Seite A
xloch_platte(
[seite_a[0], breite, dicke],
seite_a[1],
seite_a[2],
dicke
);
// Seite B
translate([dicke,0,0])
rotate([0,-90,0])
xloch_platte(
[seite_b[0], breite, dicke],
seite_b[1],
seite_b[2],
dicke
);
}
/* ... */Das Untermodul xloch_platte bekommt als Parameter die Größe des Seitenteils als dreidimensionalen Vektor (groesse), den Durchmesser (l_dm) und die Anzahl (l_anz) der Löcher sowie einen randabstand. Letzterer wird benötigt, da an der Stelle, wo die beiden Seitenteile des Winkels aufeinandertreffen, die Oberfläche der Seitenteile durch die Materialstärke der jeweils anderen Seite verkleinert wird. Da wir unsere Löcher entlang dieser Fläche verteilen wollen, müssen wir diese Verkleinerung berücksichtigen. Rein theoretisch hätten wir die Materialstärke auch aus dem Parameter groesse entnehmen können (groesse.z). Die Verwendung eines extra Parameters erleichtert hier einfach die Lesbarkeit bzw. das Verständnis.
Die Platte modellieren wir mit einem einfachen Quader, dem wir den Parameter groesse übergeben (cube(groesse);). Die Löcher erstellen wir mit einer For-Schleife und ziehen diese dann mittels der Booleschen Differenzoperation von der Platte ab. In diesem Beispiel lassen wir die For-Schleife von 1 bis zur Anzahl der Löcher laufen (x = [1:l_anz]) und rechnen die tatsächliche Position des jeweiligen Loches erst in der Verschiebe-Transformation innerhalb der Schleife aus (randabstand + x * lochabstand). Wir starten hierbei immer mit dem Randabstand und addieren dann die jeweils passende Zahl an Lochabständen auf. Den Lochabstand haben wir vor der Schleife definiert. Hierfür haben wir die verfügbare Länge (Länge der Seite minus Randabstand) durch die Anzahl der Lochzwischenräume (Anzahl der Löcher plus 1) geteilt. Für die Löcher selbst verwenden wir einen Zylinder, dem wir als Durchmesser d den Parameter l_dm zuweisen. Die Höhe h ermitteln wir aus der Höhe der Platte (groesse.z) und zwei Millimetern Zugabe, damit unser Loch auch sauber wird. Bei der Verschiebe-Transformation haben wir deswegen als Z-Verschiebung den Wert -1 angegeben. Zusammen mit der Zugabe von 2 Millimetern steht damit der Zylinder ober- und unterhalb der Platte jeweils genau 1 Millimeter vor. Der dritte Parameter $fn=18 des Zylinders ist neu. Hierbei handelt es sich um eine “Spezialvariable” von OpenSCAD mit der man die Feinheit der Geometrie des Zylinders einstellen kann. Je größer der Wert von $fn ist, desto feiner wird die Geometrie. Man sollte es an dieser Stelle nicht übertreiben. Werte von über 100 bei der Variable $fn benötigt man praktisch nie und würden die Geometrie nur unnötig rechenaufwändig machen. Man kann die Variable $fn übrigens auch “global” setzen. In diesem Fall gilt sie für alle Geometrien. Erfahrungsgemäß ist es jedoch besser, sie ganz gezielt dort einzusetzen, wo man die Feinheit der Geometrie erhöhen möchte.
Direkt unterhalb der Moduldefinition von xloch_platte benutzen wir das Modul für die beiden Seiten A und B. Da die Seite B senkrecht auf Seite A steht, müssen wir diese um 90 Grad drehen. In diesem konkreten Fall sind es minus 90 Grad, da wir gegen den Uhrzeigersinn um die Y-Achse drehen wollen. Nach der Drehung steht Seite B noch nicht ganz korrekt. Wir müssen sie noch um die Materialstärke entlang der X-Achse bewegen. Ansonsten würde unsere Seite A zu lang.
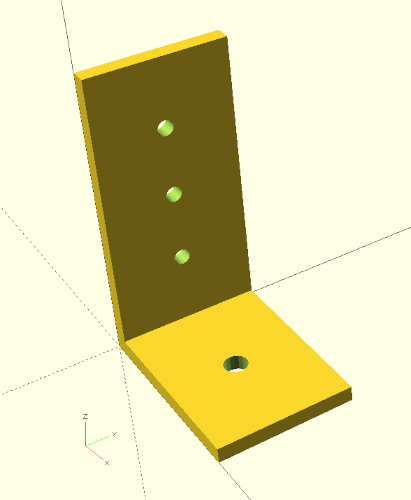
Unser Regalbodenwinkel sieht jetzt schon ziemlich passabel aus (Abbildung 3.) und wir können uns durch die Veränderung der Parameter vergewissern, dass sich unsere Geometriebeschreibung wie gewünscht verhält. Jetzt fehlen noch zwei Wangen, um unseren Winkel stabiler zu machen. Wir erstellen die Wangen zunächst aus zwei Quadern (cube), die wir unterhalb der Seiten in unserem Modul regalbodenwinkel definieren:
/* ... */
module regalbodenwinkel( seite_a, seite_b, breite, dicke ) {
module xloch_platte(groesse, l_dm, l_anz, randabstand) {
/* ... */
}
// Seite A
xloch_platte(
[seite_a[0], breite, dicke],
seite_a[1],
seite_a[2],
dicke
);
// Seite B
translate([dicke,0,0])
rotate([0,-90,0])
xloch_platte(
[seite_b[0], breite, dicke],
seite_b[1],
seite_b[2],
dicke
);
// Wangen
cube( [seite_a[0], dicke, seite_b[0]] );
translate( [0, breite-dicke, 0] )
cube( [seite_a[0], dicke, seite_b[0]] );
}
/* ... */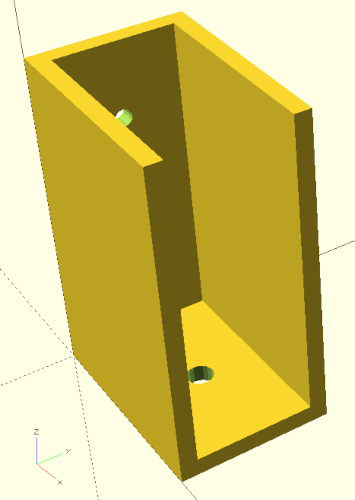
Rein technisch würden unsere Wangen schon jetzt ihren Zweck erfüllen (Abbildung 3.). Jedoch wäre es schöner, wenn unsere Regalbodenwinkel passend abgeschrägte Wangen hätten. Wir können dieses Ziel erreichen, indem wir von unserem bisherigen Winkel einen passend gedrehten Quader abziehen. Damit dies möglich wird, müssen wir unsere bisherige Geometriebeschreibung, die aus vier einzelnen Geometrien besteht (zwei mal xloch_platte und zwei mal cube) zu einer einzigen Geometrie vereinen. Dies können wir durch die Boolesche Vereinigungsoperation (engl. union) erreichen:
/* ... */
module regalbodenwinkel( seite_a, seite_b, breite, dicke ) {
module xloch_platte(groesse, l_dm, l_anz, randabstand) {
/* ... */
}
union() {
// Seite A
xloch_platte(
[seite_a[0], breite, dicke],
seite_a[1],
seite_a[2],
dicke
);
// Seite B
translate([dicke,0,0])
rotate([0,-90,0])
xloch_platte(
[seite_b[0], breite, dicke],
seite_b[1],
seite_b[2],
dicke
);
// Wangen
cube( [seite_a[0], dicke, seite_b[0]] );
translate( [0, breite-dicke, 0] )
cube( [seite_a[0], dicke, seite_b[0]] );
}
}
/* ... */Wie schon bei der Booleschen Differenz werden auch bei der Booleschen Vereinigung die einzelnen Geometrien mit Hilfe von geschweiften Klammern ({ ... }) zusammengefasst. Anstelle des Schlüsselwortes difference kommt hier union zum Einsatz. Jetzt kann von allen vier Geometrien gleichzeitig ein Quader abgezogen werden, um den gewünschten Effekt zu erreichen.
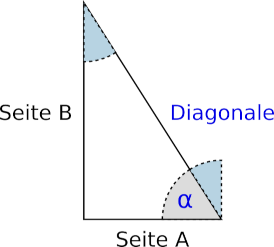
Jetzt stellt sich nur die Frage, wie groß der Quader sein muss und in welchem Winkel er gekippt werden muss (Abbildung 3.). Hier können uns vage Erinnerungen an den Matheunterricht helfen. Laut Pythagoras entspricht im rechtwinkligen Dreieck die Summe der Seitenquadrate dem Quadrat der Hauptseite. Wenn man also die Wurzel aus der Summe der Seitenquadrate zieht, bekommt man die Länge der gesuchten Diagonalen heraus. Den Winkel kann man über den Arkuscosinus ermitteln. Wie man z.B. bei Wikipedia nachschlagen kann, ist der Cosinus eines Winkels gleich der Ankathete geteilt durch die Hypothenuse. Die Hypothenuse ist hier unsere Diagonale, die Ankathete ist die Seite, an der der Winkel anliegt (im Unterschied zur Gegenkathete, die dem Winkel gegenüberliegt). Beide Werte, die Länge der Diagonalen und der Winkel der Diagonalen, können wir mit den von OpenSCAD zur Verfügung gestellten mathematischen Funktionen ausrechnen und dann für die korrekte Positionierung und Drehung des Quaders verwenden:
/* ... */
module regalbodenwinkel( seite_a, seite_b, breite, dicke ) {
module xloch_platte(groesse, l_dm, l_anz, randabstand) {
/* ... */
}
difference() {
union() {
// Seite A
xloch_platte(
[seite_a[0], breite, dicke],
seite_a[1],
seite_a[2],
dicke
);
// Seite B
translate([dicke,0,0])
rotate([0,-90,0])
xloch_platte(
[seite_b[0], breite, dicke],
seite_b[1],
seite_b[2],
dicke
);
// Wangen
cube( [seite_a[0], dicke, seite_b[0]] );
translate( [0, breite-dicke, 0] )
cube( [seite_a[0], dicke, seite_b[0]] );
}
diag = sqrt( pow(seite_a[0], 2) + pow(seite_b[0], 2) );
winkel = acos( seite_a[0] / diag );
translate( [seite_a[0], -1, 0] )
rotate( [0, -(90-winkel) , 0] )
cube( [diag, breite + 2, diag + 2] );
}
}
/* ... */Unterhalb der mit union vereinigten Geometriemenge haben wir zunächst unsere Diagonale und unseren Winkel ausgerechnet. Die Funktion sqrt berechnet die Wurzel (engl. square root) und die Funktion pow berechnet die Potenz (engl. power) einer Zahl. Bei der Potenzfunktion ist der erste Parameter die Zahl (hier: seite_a[0] bzw. seite_b[0]), die man potenzieren möchte und der zweite Parameter ist der Exponent (hier: 2). Den Winkel berechnen wir mit Hilfe des Arkuscosinus acos wie oben beschrieben aus dem Quotienten von Ankathete und Hypothenuse (hier: seite_a[0] geteilt durch diag). Im Anschluß erstellen wir einen Quader (cube), der diag lang, breite + 2 breit und diag + 2 hoch ist. Auch hier haben wir sowohl bei der Breite als auch bei der Höhe eine kleine Zugabe von zwei Millimetern, damit unsere Differenzoperation später sauber funktioniert. Wir rotieren den Quader um die Y-Achse entgegen dem Urzeigersinn (daher das -). Als Winkel verwenden wir nicht direkt den Winkel, den wir ausgerechnet haben, sondern 90 Grad minus den Winkel. Dies liegt daran, dass wir eigentlich den in Abbildung 3. blau schattierten Winkel benötigen. Wenn Sie sich besonders gut an ihren Matheunterricht erinnern, dann werden Sie jetzt vielleicht argumentieren, dass wir dann gleich den Arkussinus hätten nehmen sollen, da dieser der Wechselwinkel des von uns benötigten Winkels ist. Und Sie hätten Recht!
Nachdem wir unseren Quader rotiert haben, müssen wir ihn nur noch an die richtige Position schieben. Dies geschieht mit der Verschiebe-Transformation (translate). Wie erwartet verschieben wir unseren Quader um die Länge der Seite A entlang der X-Achse. Die Verschiebung um -1 entlang der Y-Achse dient der Absicherung der Differenzoperation und korrespondiert zu der Zugabe um 2 Millimeter in der Breite. Um die Zugabe in der Höhe brauchen wir uns an dieser Stelle nicht zu kümmern, da es reicht, wenn der Quader unseren Winkel in Kipprichtung überragt.
Nachdem der Quader jetzt in der richtigen Position ist, können wir ihn endlich von unserer Regalwinkelgeometrie abziehen. Hierzu fassen wir die zuvor erstellte Vereinigung (union) und unseren gerade erstellten Quader wieder in ein paar geschweifte Klammern ein ({ ... }) und stellen dem ganzen die Boolesche Differenzoperation (difference) voran. Geschafft!
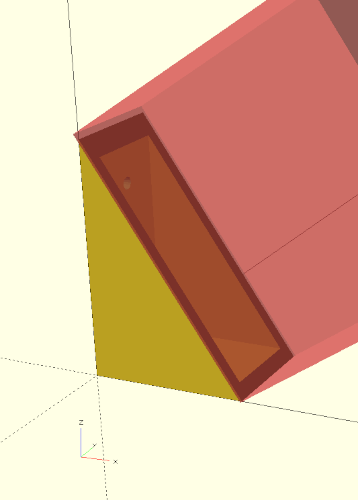
#Ein kleiner Tipp: wenn wir die Position unseres Quaders jetzt noch einmal kontrollieren wollen, ohne ihn erst wieder aus der Booleschen Differenzoperation herauslösen zu müssen, können wir dem Quader (cube) temporär ein # voranstellen. Wenn wir nun eine Vorschau berechnen lassen, wird der Quader in einer halbtransparenten Farbe dargestellt (Abbildung 3.).
Nehmen wir einmal an, wir haben unseren Regalbodenwinkel mit einem 3D-Drucker hergestellt und wollen ihn nun an der Wand montieren. Wäre es nicht praktisch, wenn wir jetzt eine Bohrschablone zum ausdrucken hätten? Zu diesem Zweck können wir eine 3D zu 2D Projektion nutzen, die in OpenSCAD über die Projektionstransformation (engl. projection) zur Verfügung steht:
/* ... */
projection(cut = true)
regalbodenwinkel(
seite_a = [50, 6, 1],
seite_b = [75, 4, 3],
breite = 35,
dicke = 4
);Die Projektionstransformation wirkt wie jede Transformation auf das jeweils nachfolgende Element und projiziert dieses auf die X-Y-Ebene. Dies ergibt so etwas wie den zweidimensionalen Schatten der Geometrie. Übergibt man der Projektionstransformation den Parameter cut = true (so wie hier), dann wird die Geometrie in der X-Y-Ebene geschnitten und nur der Schnitt wird angezeigt. Im Falle unseres Regalbodenwinkels führen beide Varianten zum selben Ergebnis. Damit der Schnitt auch wirklich als 2D Geometrie angezeigt wird, muss man übrigens eine vollständige Berechnung anstoßen (F6) und nicht nur eine Vorschau (F5). Nach der Berechnung (F6) kann die 2D-Geometrie als SVG-Grafik exportiert (File -> Export -> Export as SVG) und mit einem Grafikprogramm (z.B. Inkscape) gedruckt werden werden.
Wenn wir nun auch eine Bohrschablone von Seite B haben wollen, müssen wir unseren Winkel vorher um 90 Grad gegen den Uhrzeigersinn um die Y-Achse drehen:
/* ... */
projection(cut = true)
rotate( [0, -90, 0] )
regalbodenwinkel(
seite_a = [50, 6, 1],
seite_b = [75, 4, 3],
breite = 35,
dicke = 4
);Nun könnte man es dabei belassen und je nach Bedarf die Zeilen mit der Projektion und Rotation ein- bzw. auskommentieren. Alternativ können wir jedoch auch ein spezielles Modul definieren, dass auf Anfrage zwischen 3D Geometrie und Bohrschablonen hin- und herschalten kann:
/* ... */
module ausgabe(schablonen = false) {
if (schablonen) {
projection(cut = true)
children(0);
translate( [-0.01, 0, 0] )
projection(cut = true)
rotate( [0, -90, 0] )
children(0);
} else {
children(0);
}
}
ausgabe(schablonen = false)
regalbodenwinkel(
seite_a = [50, 6, 1],
seite_b = [75, 4, 3],
breite = 35,
dicke = 4
);Das Modul ausgabe hat einen Parameter schablonen. Wenn dieser auf wahr (engl. true) gesetzt wird, dann werden die Bohrschablonen der Seiten A und B erzeugt (Abbildung 3.). Wird der Parameter auf falsch (engl. false) gesetzt, wird die normale 3D-Geometrie erzeugt. Innerhalb des Moduls ausgabe wird dies mit einer If-Fallunterscheidung beschrieben. Der Ausdruck if (schablonen) ist hierbei eine Abkürzung von if (schablonen == true). Die spannende Frage ist jedoch, wie denn unsere Regalbodenwinkel-Geometrie in das Modul ausgabe kommt. Dies geschieht durch das Schlüsselwort children. Hiermit erhalten wir Zugriff auf das unserem Modul nachfolgende Element! Der Parameter 0 gibt dabei an, dass wir das erste Element haben wollen. Würde hinter unserem Modul eine in geschweiften Klammern ({ ... }) eingefasste Geometriemenge stehen, könnten wir auch auf weitere Elemente zugreifen. Wieviele Elemente es gibt, würde uns in diesem Fall die “Spezialvariable” $children verraten. In unserem Fall wissen wir jedoch, dass es nur ein nachfolgendes Element (unseren Regalbodenwinkel) gibt. Daher benötigen wir $children an dieser Stelle nicht.
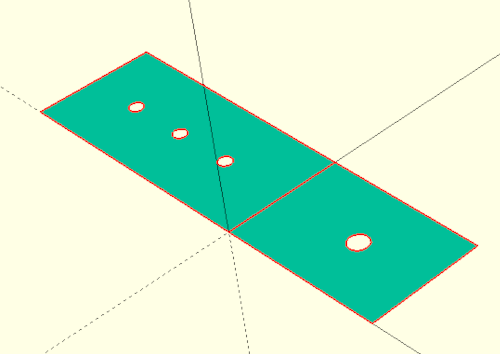
Grundsätzlich ermöglicht uns das Schlüsselwort children, Module zu definieren, die sich wie Transformationen verhalten. Aus Erfahrung kann man sagen, dass man diese Fähigkeit nicht allzu oft benötigt. Es gibt jedoch Situationen, wo man sehr elegante Lösungen für ansonsten aufwendige Geometriebeschreibungen damit erreichen kann.
Wenn wir unsere Geometriebeschreibung mit einem 3D-Drucker ausdrucken wollen, dann müssen wir unsere Geometrie zunächst berechnen (F6). Dies kann je nach Geometrie auch mal einige Minuten dauern. Haben Sie hier einfach etwas Geduld. Wenn die Berechnung fertig ist, können Sie die entstandene Geometrie exportieren (File -> Export -> Export as …). Ein typisches Format hierfür ist .stl. Die .stl-Datei können Sie dann in eine sogenannte Slicer-Software (to slice -> in Scheiben schneiden) einladen und für den 3D-Druck vorbereiten.
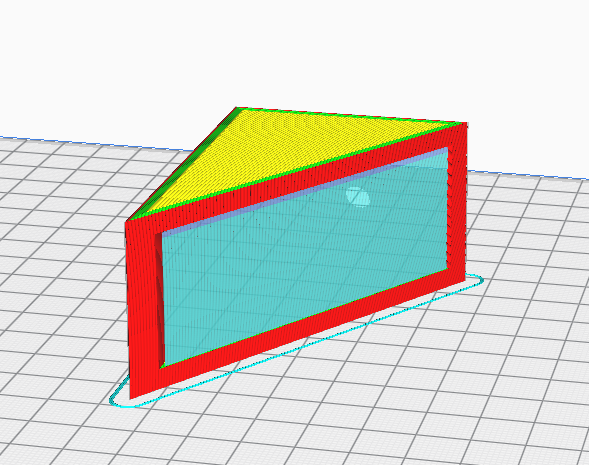
Innerhalb der Slicer-Software stellt sich die Frage, in welcher Ausrichtung man den Regalbodenwinkel drucken möchte. Da 3D-gedruckte Bauteile schichtweise entstehen, ist die Stabilität der Bauteile innerhalb einer Schicht deutlich größer als zwischen den Schichten. Insbesondere Scherkräfte, die auf die Schichten wirken, können ein Bauteil zerbrechen lassen. Für unseren Regalbodenwinkel wäre es daher am besten, ihn auf der Seite liegend zu drucken. Ein Nachteil dieser Ausrichtung ist, dass man dann vermutlich eine Stützstruktur innerhalb des Bauteils benötigt, die die oben liegende Wange beim Druck stabilisiert (Abbildung 3.).
Eine alternative Ausrichtung, die ggf. ohne eine Stützstruktur auskommt und dennoch zu einem stabilen Bauteil führt, besteht darin, den Winkel auf der abgeschrägten Seite liegend zu drucken. Den passenden Winkel direkt in der Slicer-Software einzustellen, kann etwas aufwendig sein. Hier lohnt es sich, die Geometrie bereits passend gedreht aus OpenSCAD heraus zu exportieren. Hierzu können wir unser Modul regalbodenwinkel noch einmal erweitern:
module regalbodenwinkel( seite_a, seite_b, breite, dicke, drehen = false ) {
module xloch_platte(groesse, l_dm, l_anz, randabstand) {
/* ... */
}
diag = sqrt( pow(seite_a[0], 2) + pow(seite_b[0], 2) );
winkel = asin(seite_a[0] / diag);
rotate( [0, drehen ? 90 + winkel : 0, 0] )
difference() {
union() {
// Seite A
xloch_platte(
[seite_a[0], breite, dicke],
seite_a[1],
seite_a[2],
dicke
);
// Seite B
translate([dicke,0,0])
rotate([0,-90,0])
xloch_platte(
[seite_b[0], breite, dicke],
seite_b[1],
seite_b[2],
dicke
);
// Wangen
cube( [seite_a[0], dicke, seite_b[0]] );
translate( [0, breite-dicke, 0] )
cube( [seite_a[0], dicke, seite_b[0]] );
}
translate([seite_a[0],-1,0])
rotate([0,-(winkel),0])
cube([diag,breite+2,diag+2]);
}
}Wir geben unserem Modul einen weiteren Parameter drehen, dem wir den Standardwert false (dt. falsch) geben. Anschließend ziehen wir die Berechnung der Diagonale und des Winkels nach oben vor die Boolesche Differenz (difference) und drehen unser ganzes Objekt um die Y-Achse im Uhrzeigersinn um 90 + winkel Grad wenn der Parameter drehen wahr (engl. true) ist. Ansonsten drehen wir nicht (0 Grad).
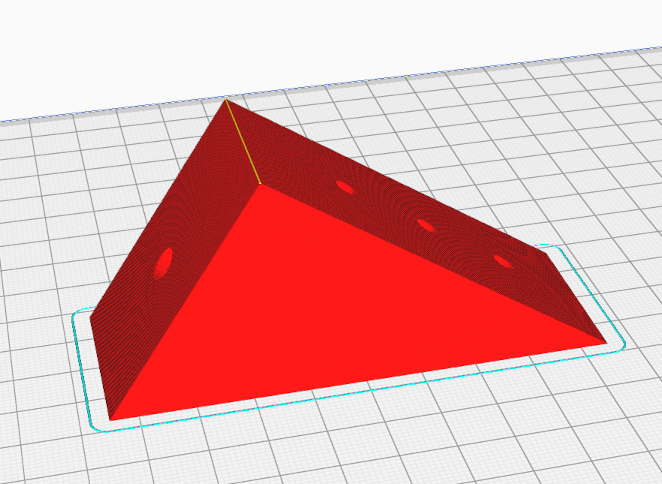
Exportieren wir nun unsere Geometrie erneut als .stl-Datei, dann liegt unser Bauteil direkt in der richtigen Ausrichtung in der Slicer-Software und kann ohne Stützstruktur und dennoch als stabiles Objekt gedruckt werden (Abbildung 3.).
Nachdem Sie den Regalbodenwinkel gedruckt haben, ist es ratsam, einmal alle Maße des gedruckten Objektes nachzumessen. Insbesondere bei den Löchern kann es dazu kommen, dass diese nicht maßgetreu gedruckt wurden. Wenn dies der Fall ist, können Sie jetzt von der Stärke der parametrischen Modellierung profitieren. Sie können einfach in den Parametern des Regalbodenwinkels die Durchmesser entsprechend anpassen und auf Knopfdruck eine angepassten Geometrie berechnen lassen.