

Wie eingangs erwähnt werden in OpenSCAD geometrische Modelle durch eine textuelle Spezifikation beschrieben. Auf den ersten Blick ähnelt diese textuelle Beschreibung einem Programm, welches in einer Programmiersprache wie Javascript oder C geschrieben wurde. Gerade wenn man ein wenig Programmiererfahrung hat, kann diese augenscheinliche Ähnlichkeit zu einigen Missverständnissen und fehlgeleiteten Intuitionen führen. Auch wenn die textuelle Beschreibung der Geometrien in OpenSCAD an klassischen Programmcode erinnert, so handelt es sich nicht um ein Programm. Es handelt sich vielmehr um die Spezifikation einer geometrischen Struktur. Im Laufe der folgenden Abschnitte wird dieser Unterschied Schritt für Schritt klarer werden. Der Fokus dieses Kapitels liegt auf der Vermittlung der wesentlichen Konzepte und Funktionsweisen von OpenSCAD anhand ausgewählter Beispiele. Eine vollständige Beschreibung aller Funktionen findet sich am Ende des Buches sowie in der Online-Dokumentation von OpenSCAD.
Lassen Sie uns nun endlich loslegen und ein wenig ausprobieren, wie man denn nun eine Geometrie in OpenSCAD beschreiben kann. Wenn Sie es nicht bereits getan haben, wäre jetzt ein guter Zeitpunkt, OpenSCAD mit einer leeren bzw. neuen Datei zu starten. Das OpenSCAD-Programmfenster sollte nun den internen Editor, das Ausgabefenster und die Konsolenansicht zeigen. Den Customizer können sie vorerst ausblenden.
Das Fundament einer jeden Geometrie in OpenSCAD sind die sogenannten Primitive. Dies sind zwei- oder dreidimensionale Grundformen, die wir als Bausteine für unser Modell benutzen können. Lassen Sie uns eine einfache Kugel (engl. sphere) erstellen. Geben Sie hierfür im Editorfenster folgendes ein:
sphere(10);Wenn Sie nun eine Vorschau berechnen lassen (Taste F5), dann sollte im Ausgabefenster eine Kugel mit einem Radius von 10 Millimetern angezeigt werden.
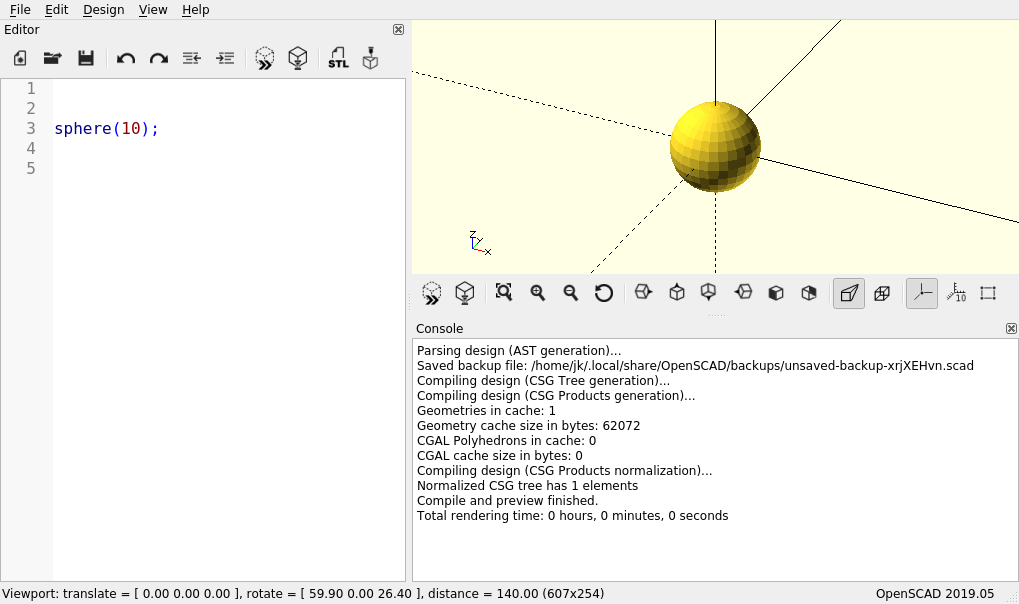
Schauen Sie auch einmal auf das Konsolenfenster. Dort sollten Sie eine ganze Reihe an Ausgaben finden, die im Rahmen der Vorschau produziert wurden. In der vorletzten Zeile dieser Ausgabe sollte ein Compile and preview finished. (dt. Kompilierung und Vorschau beendet) stehen (Abbildung 2.).
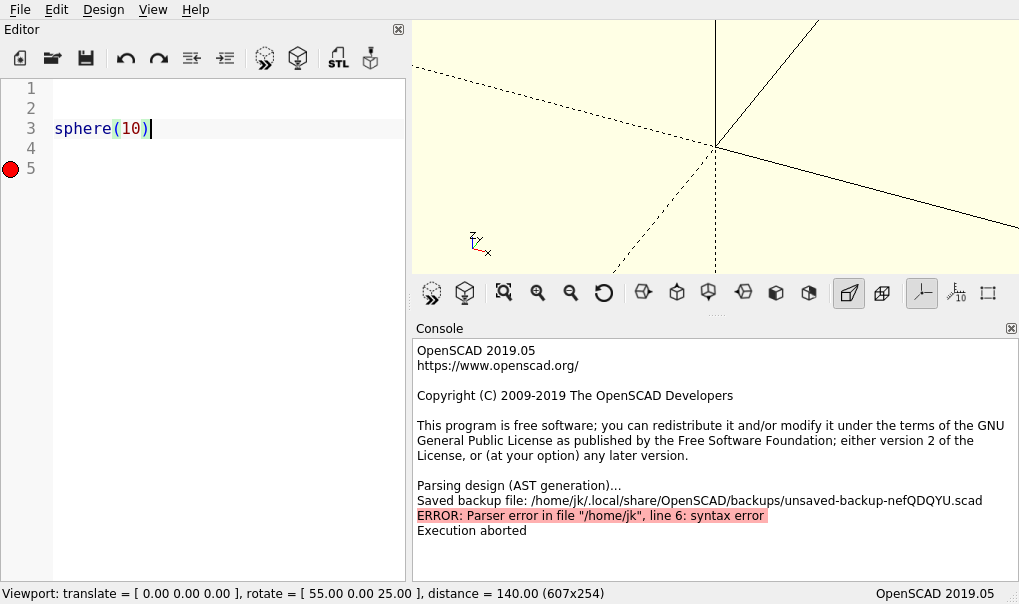
Wenn anstelle dessen ein rot markiertes ERROR in der Ausgabe steht, lief irgendetwas schief (Abbildung 2.). Vielleicht haben Sie sich vertippt? Oder vielleicht das Semikolon am Ende der Zeile vergessen? Haben Sie sphere vielleicht mit einem großen S anstatt eines kleinen geschrieben? Versuchen Sie den Fehler zu finden und probieren Sie die Vorschauberechnung (F5) erneut.
Jede Grundform in OpenSCAD hat einen eindeutigen Namen, dem immer eine Liste von Parametern in runden Klammern und ein abschließendes Semikolon folgt. Im obigen Beispiel ist der Radius der Kugel der erste Parameter. Jeder Parameter hat auch eine Bezeichnung und im Allgemeinen ist es besser, diese Bezeichnung mit anzugeben. Im Falle der Kugel hat der Radius-Parameter die Bezeichnung r und eine Verwendung dieser Parameterbezeichnung würde so aussehen:
sphere(r = 10);Auch wenn es etwas mehr Tipparbeit ist, hat die Verwendung der Parameterbezeichnung gleich zwei Vorteile. Zum einen wird die Geometriebeschreibung lesbarer. Zum anderen muss man sich nicht an die exakte Reihenfolge der Parameter erinnern, falls eine Grundform mehrere Parameter hat. Dies ist auch bei der Kugel der Fall. Anstelle des Radius kann man die Kugel auch mit einem Durchmesser definieren:
sphere(d = 10);Probieren Sie es aus (F5). Die Kugel sollte nun nur noch halb so groß im Ausgabefenster erscheinen. Was passiert wohl, wenn man sowohl einen Radius als auch einen Durchmesser angibt?
sphere(r = 10, d = 10);Wenn man nun die Vorschau berechnen lässt (F5), dann verändert sich die Kugel nicht und in der Konsole wird eine gelb hinterlegte Warnung ausgegeben: Ignoring radius variable ‘r’ as diameter ’d' is defined too (dt. Ignoriere Radiusvariable ‘r’ da der Durchmesser ’d' ebenfalls definiert ist). Bei der Kugel hat also der Durchmesser Vorrang, wenn zusätzlich auch ein Radius angegeben wurde. Die Reihenfolge der Parameter spielt hier keine Rolle.
Falls Sie Programmiererfahrung haben, mag der Ausdruck sphere(r=10); Sie an einen Methodenaufruf erinnern. Im Kontext von OpenSCAD ist diese Intuition leider eher hinderlich als nützlich. Es ist besser, den Ausdruck nicht als Methodenaufruf zu interpretieren, sondern als eine Aussage über die Existenz einer konkreten Geometrie. In diesem Sinne besagt der Ausdruck sphere(r=10); in etwa: Es existiert eine Kugel mit Radius 10mm.
Bisher haben wir den Radius unserer Kugel mit einem direkten Wert angegeben. Wenn wir wissen, dass wir diesen Wert nie wieder anpassen müssen bzw. wollen, ist dies vollkommen in Ordnung. Möchten wir den Radius der Kugel in unserem Modell konfigurierbar machen, dann sollten wir dem Radius einen eigenen Namen geben. Dies können wir über eine Variable erreichen:
kugelradius = 10;
sphere(r = kugelradius);In größeren Projekten ist es nützlich, alle Konfigurationsvariablen zu Beginn der Modelldatei zu sammeln. So hat man alle Einstellmöglichkeiten im Blick. Darüber hinaus sollte man es sich gleich angewöhnen, die Variablen (und an geeigneten Stellen auch die Geometrie) zu kommentieren. Einzeilige Kommentare kann man mit // einleiten. In diesem Fall wird alles bis zum Ende der Zeile als Kommentar gewertet. Braucht man mehr Platz, kann man einen Kommentarblock mit /* beginnen und mit */ beenden:
/*
Dies ist ein OpenSCAD Testprojekt
---------------------------------
*/
kugelradius = 10; // Ein ganz wichtiger Radius
// Die zentrale Kugel unseres Modells
sphere(r = kugelradius);Auch an dieser Stelle kann Programmiererfahrung hinderlich sein. Unser Modell sieht ja jetzt noch mehr aus wie ein typisches sequentielles Programm! Dem ist aber nicht so. Eine Variable in OpenSCAD repräsentiert keinen Speicherbereich, der im Verlauf eines Programms unterschiedliche Werte annehmen kann, sondern ist erneut nur eine Existenzaussage: Es existiert der Wert 10 mit der Bezeichnung “kugelradius”. Was passiert, wenn wir eine Variable zweimal benutzen? Probieren wir es aus!
kugelradius = 10;
sphere(r = kugelradius);
kugelradius = 20;Wenn wir nun die Vorschau berechnen lassen (F5), dann sehen wir, dass die Kugel den Radius 20 annimmt. Gleichzeitig sehen wir in der Konsole eine Warnung: kugelradius was assigned on line 1 but was overwritten on line 5 (dt. kugelradius wurde in Zeile 1 zugewiesen, wurde jedoch in Zeile 5 überschrieben). Wir sehen, dass man einer Variable nur einen Wert geben kann. OpenSCAD verwendet hierfür immer den zuletzt gesetzten Wert (hier 20). Dies bedeutet auch, dass eine Variable nicht “vor” ihrer Verwendung definiert werden muss. Das “vor” steht in Anführungsstrichen, da es in einer OpenSCAD-Geometriebeschreibung kein zeitliches “vor” in diesem Sinne gibt.
Bei der Beschreibung von Werten durch Variablen ist man nicht darauf beschränkt, nur einzelne Werte zu verwenden. Nehmen wir einmal an, die Maße in unserem Modell bräuchten noch einen Korrekturwert. Dies könnten wir so umsetzen:
korrekturwert = 0.7;
kugelradius = 10 + korrekturwert;
seitenrand = 5 + korrekturwert;
tiefe = 25 + korrekturwert;
// ... noch viel mehr Konfigurationsvariablen mit korrekturwertSoweit so gut. Nehmen wir an, wir stellen plötzlich fest, das wir auch noch einen Korrekturfaktor brauchen! Das könnten wir so umsetzen:
korrekturwert = 0.7;
korrekturfaktor = 1.05;
kugelradius = (10 + korrekturwert) * korrekturfaktor;
seitenrand = ( 5 + korrekturwert) * korrekturfaktor;
tiefe = (25 + korrekturwert) * korrekturfaktor;Sie sehen schon, dass es irgendwie aufwendig ist, jede Konfigurationsvariable für diese Veränderung anfassen zu müssen. Eine elegantere Lösung besteht darin, eine Funktion für die Korrektur zu verwenden:
korrekturwert = 0.7;
korrekturfaktor = 1.05;
function korrektur(x) = (x + korrekturwert) * korrekturfaktor;
kugelradius = korrektur(10);
seitenrand = korrektur( 5);
tiefe = korrektur(25);Falls wir nun die Korrektur in unserem Beispiel noch einmal anpassen müssen, dann brauchen wir fortan nur noch die Funktion korrektur(x) zu ändern. Funktionsdefinitionen werden mit dem Schlüsselwort function eingeleitet, gefolgt von einem eindeutigen Namen für die Funktion (hier korrektur) und einer Parameterliste in runden Klammern (hier (x)). Die Funktion selbst wird nach einem Gleichheitszeichen geschrieben und endet stets mit einem Semikolon. Neben unseren eigenen Funktionen bietet OpenSCAD eine ganze Reihe vordefinierter Funktionen an (z.B. sin(), cos(), round()), von denen wir einige im Laufe dieses Buches kennenlernen werden.
Bevor wir mit dem nächsten Abschnitt weitermachen, sollten wir kurz rekapitulieren, welche Grundbausteine wir kennengelernt haben:
Im vorherigen Abschnitt haben wir die Grundform Kugel in unserer Modellbeschreibung verwendet. Jetzt benutzen wir zur Abwechslung mal einen Würfel (engl. cube):
cube(size = 10, center = true);Über den Parameter size definieren wir die Kantenlänge des Würfels. Der Parameter center bestimmt, wo der Würfel seinen Ursprung hat (Abbildung 2.).
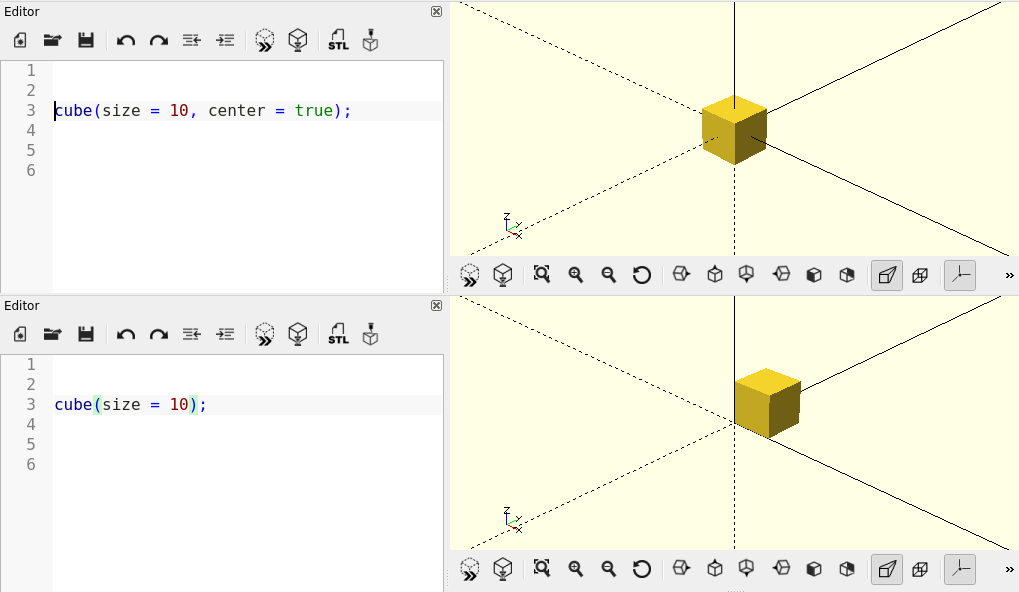
Wie die Kugel zuvor wird der Würfel genau im Ursprung des Koordinatensystems angezeigt. Im Anzeigefenster wird das Koordinatensystem durch drei senkrecht zueinander stehende Linien dargestellt, die jeweils die X-, Y- und Z-Achse repräsentieren. Die positiven Bereiche der einzelnen Achsen werden über durchgezogene Linien dargestellt. Die negativen Bereiche durch gestrichelte Linien. Mit der Tastenkombination STRG + 2 können die Koordinatenachsen ein- und ausgeblendet werden. Achten Sie auch auf das kleine, beschriftete Koordinatenkreuz unten links im Anzeigefenster, welches als Orientierungshilfe dient.
Wenn wir nun unseren Würfel an eine andere Position bewegen wollen, müssen wir hierfür eine sogenannte Transformation verwenden. In diesem Fall eine Verschiebung bzw. Translation:
translate( [20,0,0] ) cube(10,true);Eine Transformation (hier translate( [20,0,0] )) wirkt sich immer auf das nachfolgende Element aus. In diesem Fall auf unseren Würfel. Als einzigen Parameter bekommt die Transformation translate einen dreidimensionalen Vektor, der die gewünschte Verschiebungsdistanz in X-, Y- und Z-Richtung beschreibt. Vektoren werden in OpenSCAD mit eckigen Klammern geschrieben und die Zahlen werden durch Kommata getrennt.
An dieser Stelle muss auf ein ganz zentrales Funktionsprinzip von OpenSCAD hingewiesen werden. Der gesamte Ausdruck translate(...) cube(...); wird ein eigenständiges geometrisches Objekt, dass so wie jede andere Grundform (Kugel, Würfel, etc.) verwendet werden kann! Dies bedeutet insbesondere, dass wir diesem neuen Objekt weitere Transformationen voran stellen können, z.B. eine Drehung (engl. rotation):
rotate( [0,0,45] ) translate( [20,0,0] ) cube(10,true);Die Transformation rotate dreht ein geometrisches Objekt um den Ursprung. Als Parameter bekommt die Transformation erneut einen dreidimensionalen Vektor. In diesem Fall enthält der Vektor die gewünschten Rotationswinkel um die X-, Y- und Z-Achse. Und auch hier wird wieder der gesamte Ausdruck rotate(...) translate(...) cube(...); ein neues, eigenständiges geometrisches Objekt. Da das Semikolon das Ende des Objektes markiert, kann man die Transformationen auch in die Zeilen über der Grundform (hier: cube) schreiben, um eine allzu lange Zeilenlänge zu vermeiden.
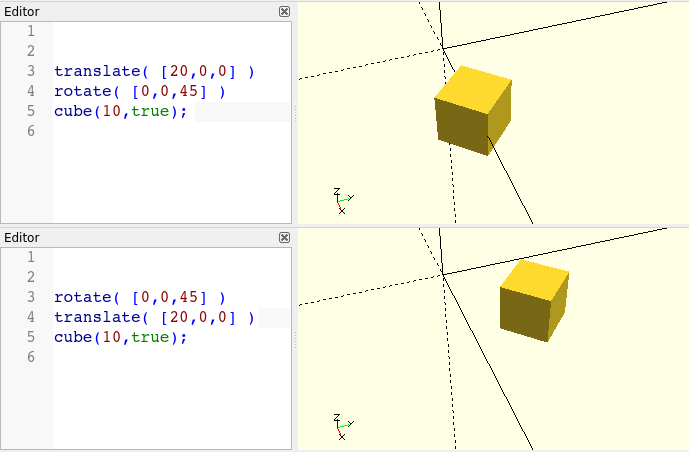
Abbildung 2. illustriert, wie unser Endergebnis von der Reihenfolge der Transformationen abhängt. Da die Transformationen in OpenSCAD sich immer auf den Ursprung beziehen, macht es einen großen Unterschied, ob man ein Objekt erst verschiebt und dann rotiert, oder umgekehrt.
Mit geometrischen Grundformen und Transformationen sind wir nun auf einem Stand, der uns in etwa die Modellierungsmöglichkeiten gibt, die man zu Kinderzeiten mit Bausteinen hatte. Im nächsten Abschnitt werden wir diese Fähigkeiten deutlich erweitern.
Nehmen wir einmal an, dass wir eine 5mm starke Platte mit einem Maß von 10cm x 5cm modellieren wollen. Dies könnten wir auf die folgende Art und Weise machen:
// Maße in mm [Breite, Tiefe, Höhe]
platte = [100,50,5];
cube( platte );Wir definieren uns einen dreidimensionalen Vektor platte, der die Maße unserer Platte enthält und übergeben diesen Vektor als Parameter an die Grundform cube (Abbildung 2.).
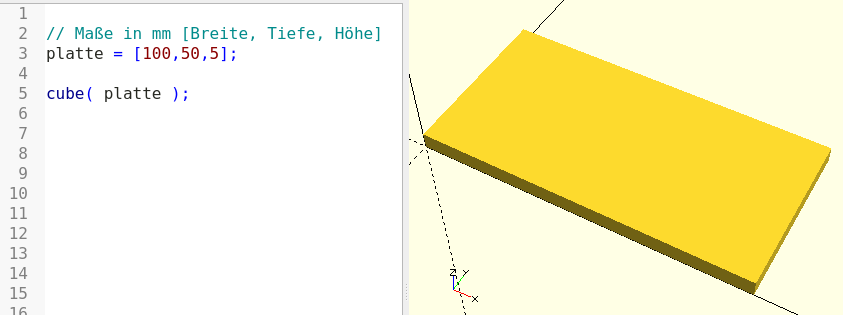
Angenommen, wir möchten nun an den Ecken der Platte vier Bohrlöcher modellieren. Fangen wir damit an, dass wir erst einmal zwei Variablen definieren. Eine für den Durchmesser der Bohrlöcher und eine für den Abstand der Bohrlöcher vom Rand der Platte:
// Maße in mm [Breite, Tiefe, Höhe]
platte = [100,50,5];
bohrloch_abstand = 4;
bohrloch_durchmesser = 6;
cube( platte );Als nächstes müssen wir OpenSCAD beschreiben, welche Form unsere Löcher haben sollen. Dafür eignet sich die Grundform Zylinder (engl. cylinder):
// Maße in mm [Breite, Tiefe, Höhe]
platte = [100,50,5];
bohrloch_abstand = 4;
bohrloch_durchmesser = 6;
cube( platte );
cylinder( d = bohrloch_durchmesser, h = platte.z );Der Parameter d der Grundform cylinder bestimmt den Durchmesser, der Parameter h bestimmt die Höhe. Da der Zylinder unser Bohrloch beschreiben soll, übergeben wir für d unsere Variable bohrloch_durchmesser und für h die Z-Koordinate des Plattenvektors, in der die Höhe bzw. Stärke der Platte definiert ist. Anstelle von platte.z hätte man hier auch platte[2] schreiben können.
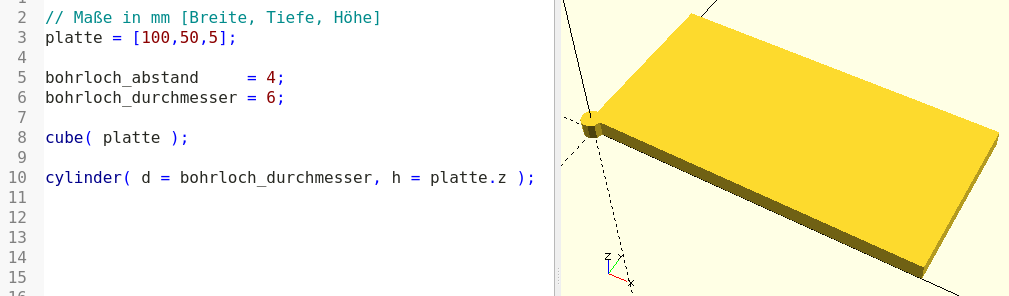
Noch befindet sich unser Bohrlochzylinder am falschen Platz (Abbildung 2.) und ist überdies nicht gut von der modellierten Platte zu unterscheiden. Lassen Sie uns den Zylinder verschieben und ihm eine andere Farbe geben:
// Maße in mm [Breite, Tiefe, Höhe]
platte = [100,50,5];
bohrloch_abstand = 4;
bohrloch_durchmesser = 6;
cube( platte );
translate
([
bohrloch_abstand + bohrloch_durchmesser/2,
bohrloch_abstand + bohrloch_durchmesser/2,
0
])
color( "red" )
cylinder( d = bohrloch_durchmesser, h = platte.z );Wir wenden zunächst die Transformation color (dt. einfärben) an und färben damit den Zylinder rot (engl. red). Den roten Zylinder verschieben wir dann mittels der Transformation translate in die untere linke Ecke der Platte. Um unsere Modellbeschreibung etwas übersichtlicher zu halten, haben wir den Parameter der Transformation über mehrere Zeilen verteilt.
Bevor wir uns um die restlichen drei Bohrlochzylinder kümmern, machen wir erstmal unser erstes Loch in die Platte. Dies geht mit einer sogenannten Booleschen Operation (engl. boolean operation), die zwei oder mehr Geometrien miteinander kombinieren kann. In OpenSCAD stehen drei Arten von Boolescher Operation zur Verfügung: Differenz (engl. difference), Vereinigung (engl. union) und Schnitt (engl. intersection). Für unser Bohrloch benötigen wir die Differenzoperation, da wir den Zylinder von der Platte “abziehen” wollen:
// Maße in mm [Breite, Tiefe, Höhe]
platte = [100,50,5];
bohrloch_abstand = 4;
bohrloch_durchmesser = 6;
difference() {
cube( platte );
translate
([
bohrloch_abstand + bohrloch_durchmesser/2,
bohrloch_abstand + bohrloch_durchmesser/2,
0
])
color( "red" )
cylinder( d = bohrloch_durchmesser, h = platte.z );
}Genau wie eine Transformation wirkt eine Boolesche Operation (hier: difference()) auf das nachfolgende Element. Da Boolsche Operationen mehrere Geometrien miteinander kombinieren, würde es wenig Sinn ergeben, wenn das nachfolgende Element nur aus einer einzelnen Geometrie bestünde - auch wenn dies prinzipiell in OpenSCAD erlaubt ist. Daher wird als nachfolgendes Element eine Geometriemenge definiert, indem man eine Reihe von geometrischen Objekten durch ein Paar geschweifter Klammern { ... } zusammenfasst. Im Falle der Differenzoperation werden vom ersten Objekt der Menge alle folgenden Objekte abgezogen.
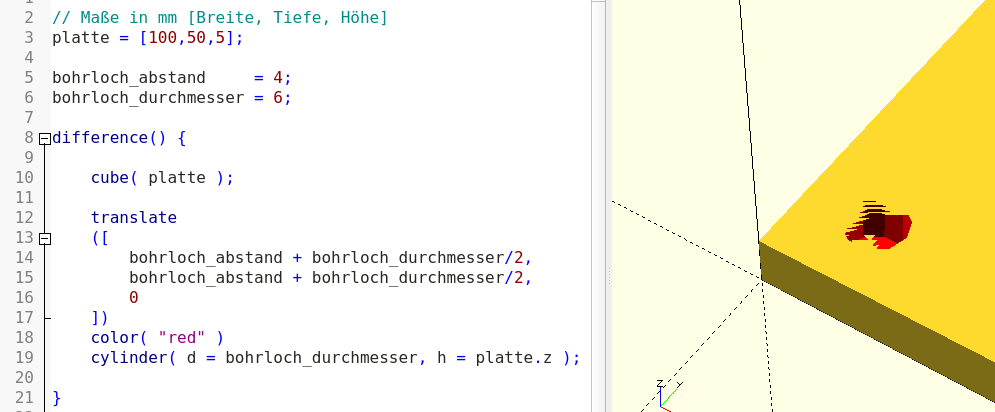
Abbildung 2. zeigt, dass unser erstes Bohrloch leider nicht ganz in Ordnung ist. Die Oberfläche an der Stelle des Lochs zeigt seltsame Defekte. Insbesondere, wenn man die Ansicht im Anzeigefenster mit der Maus verändert. Diese Defekte sind auf Rundungsfehler bei der Berechnung zurückzuführen, da die Ober- und Unterkante unseres Bohrlochzylinders bündig mit der Ober- und Unterkante der Platte abschließt. Um das Problem zu beheben, müssen wir die Höhe des Zylinders ein kleines bisschen vergrößern und ihn gleichzeitig etwas nach unten bewegen, sodass der Zylinder sowohl oben als auch unten übersteht:
// Maße in mm [Breite, Tiefe, Höhe]
platte = [100,50,5];
bohrloch_abstand = 4;
bohrloch_durchmesser = 6;
difference() {
cube( platte );
translate
([
bohrloch_abstand + bohrloch_durchmesser/2,
bohrloch_abstand + bohrloch_durchmesser/2,
-1
])
color( "red" )
cylinder( d = bohrloch_durchmesser, h = platte.z + 2);
}
Nun sieht das entstandene Loch sauber aus (Abbildung 2.). Um die Position des Zylinders zu überprüfen, kann man dem Bohrzylinder-Objekt temporär ein # in der Beschreibung voranstellen. Hierdurch wird der Zylinder halbtransparent in der Vorschau eingeblendet.
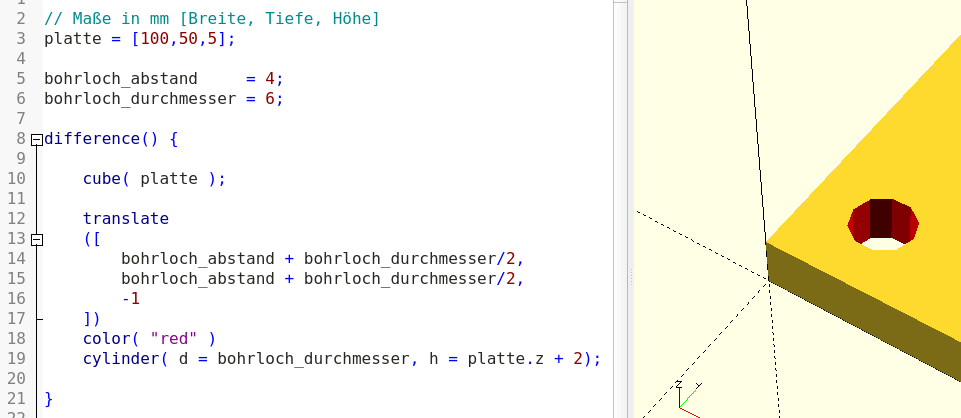
Nun können wir uns endlich um die anderen drei Bohrlöcher kümmern. Hierzu kopieren wir einfach unser bestehendes Bohrloch drei mal und passen jeweils die Position an:
// Maße in mm [Breite, Tiefe, Höhe]
platte = [100,50,5];
bohrloch_abstand = 4;
bohrloch_durchmesser = 6;
difference() {
cube( platte );
randabstand = bohrloch_abstand + bohrloch_durchmesser/2;
// Bohrloch unten links
translate
([
randabstand,
randabstand,
-1
])
color( "red" )
cylinder( d = bohrloch_durchmesser, h = platte.z + 2);
// Bohrloch unten rechts
translate
([
platte.x - randabstand,
randabstand,
-1
])
color( "red" )
cylinder( d = bohrloch_durchmesser, h = platte.z + 2);
// Bohrloch oben links
translate
([
randabstand,
platte.y - randabstand,
-1
])
color( "red" )
cylinder( d = bohrloch_durchmesser, h = platte.z + 2);
// Bohrloch oben rechts
translate
([
platte.x - randabstand,
platte.y - randabstand,
-1
])
color( "red" )
cylinder( d = bohrloch_durchmesser, h = platte.z + 2);
}Die Geometriemenge, auf die sich nun die Differenzoperation bezieht enthält nun fünf Objekte. Unsere Platte gefolgt von vier Bohrzylindern. Dies führt zum gewünschten Resultat (Abbildung 2.). Jedoch ist nun unsere Geometriebeschreibung sehr umfangreich und damit etwas unübersichtlich geworden.
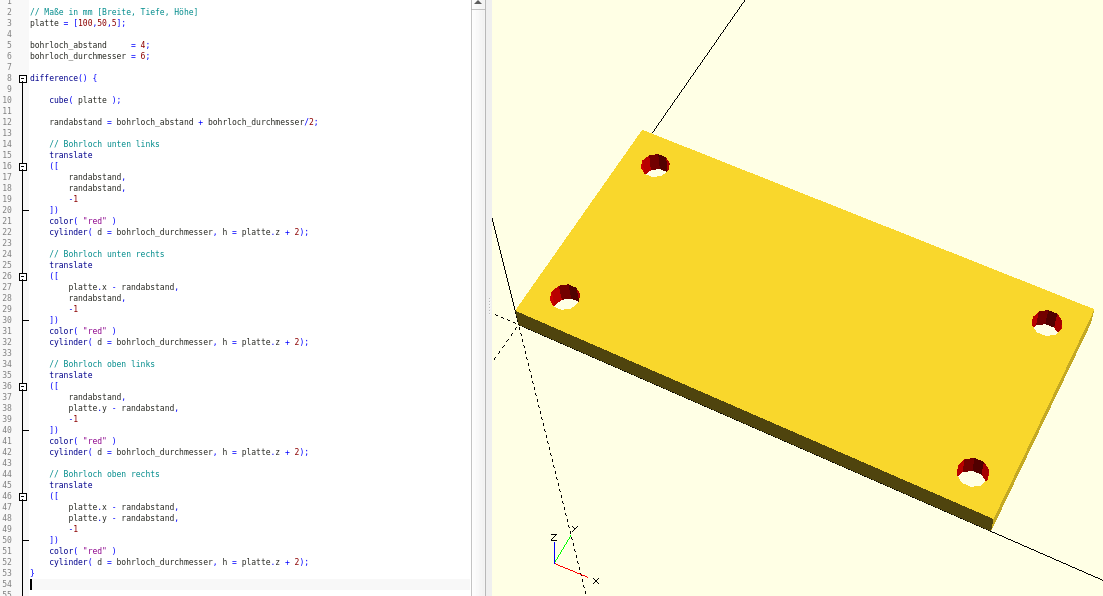
Immer wenn man sich dabei erwischt, einen Spezifikationsblock mehrfach zu kopieren, um ihn dann jeweils nur minimal zu verändern, ist das ein starker Hinweis darauf, dass es vermutlich eine bessere Möglichkeit gibt, die aktuelle Geometrie zu beschreiben. Dies ist auch in diesem Fall so. Anstatt das Bohrloch viermal zu kopieren, können wir die vier Instanzen des Bohrlochs auch durch eine Schleife beschreiben:
// Maße in mm [Breite, Tiefe, Höhe]
platte = [100,50,5];
bohrloch_abstand = 4;
bohrloch_durchmesser = 6;
difference() {
cube( platte );
randabstand = bohrloch_abstand + bohrloch_durchmesser/2;
x_werte = [randabstand, platte.x - randabstand];
y_werte = [randabstand, platte.y - randabstand];
// Bohrlöcher
for (x = x_werte, y = y_werte)
translate( [x, y, -1] )
color( "red" )
cylinder( d = bohrloch_durchmesser, h = platte.z + 2);
}Schleifen werden in OpenSCAD durch das Schlüsselwort for (dt. für) gefolgt von einer oder mehreren Schleifenvariablen in runden Klammern beschrieben. Den Schleifenvariablen kann entweder ein Feld (engl. array) oder eine Spanne (engl. range) zugewiesen werden. Felder haben wir in Form von Vektoren bereits kennengelernt. Sie unterscheiden sich in ihrer Definition nicht. Eine Spanne sieht in OpenSCAD einem Feld sehr ähnlich: [Startwert : Endwert] bzw. [Startwert : Schrittweite : Endwert]. Man kann eine Spanne als implizites Feld verstehen, bei dem man nur Start- und Endwert angibt und die dazwischen liegenden Werte automatisch berechnet werden. Wird keine Schrittweite angegeben, wird eine Schrittweite von 1 angenommen.
Genau wie Transformationen und Boolesche Operationen beziehen sich For-Schleifen auf das nachfolgende Element. Dieses wird als Vorlage genutzt, um für jede mögliche Kombination der Schleifenvariablen ein neues geometrisches Objekt zu erzeugen. Werden die Schleifenvariablen in der Vorlage benutzt, werden die entsprechenden Werte aus dem zugehörigen Feld bzw. der zugehörigen Spanne jeweils eingesetzt. Das “Ergebnis” einer For-Schleife ist nicht eine Geometriemenge, sondern eine einzelne, vereinigte Geometrie.
Unser Beispiel verwendet die Felder x_werte und y_werte, die den Schleifenvariablen x und y zugewiesen werden. Hier ist eine Version, die zwei Spannen verwendet:
// Maße in mm [Breite, Tiefe, Höhe]
platte = [100,50,5];
bohrloch_abstand = 4;
bohrloch_durchmesser = 6;
difference() {
cube( platte );
randabstand = bohrloch_abstand + bohrloch_durchmesser/2;
x_lochdistanz = platte.x - 2*randabstand;
y_lochdistanz = platte.y - 2*randabstand;
x_werte = [randabstand : x_lochdistanz : platte.x - randabstand];
y_werte = [randabstand : y_lochdistanz : platte.y - randabstand];
// Bohrlöcher
for (x = x_werte, y = y_werte)
translate( [x, y, -1] )
color( "red" )
cylinder( d = bohrloch_durchmesser, h = platte.z + 2);
}Die Verwendung zweier Spannen ist etwas aufwendiger als die vorherige Version, die zwei Felder nutzte. Dies liegt daran, dass wir erst die passenden Schrittweiten x_lochdistanz und y_lochdistanz berechnen müssen. Im nächsten Abschnitt werden wir diesen Mehraufwand gewinnbringend nutzen. Zuvor lohnt es sich, einmal den Customizer anzuschauen (Abbildung 2.).
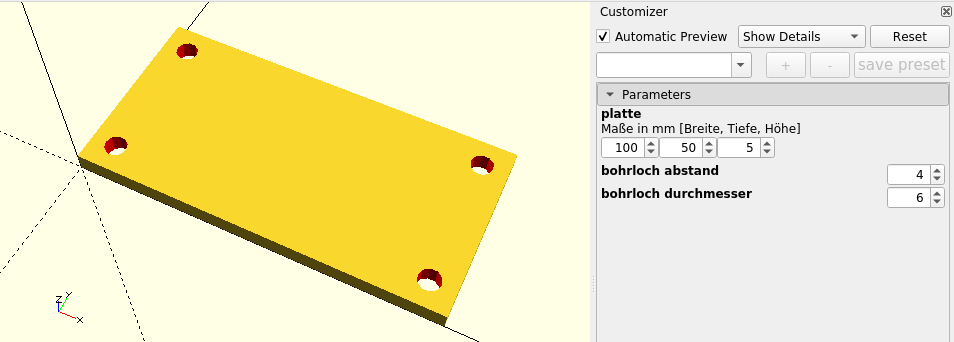
Unsere Variablen platte, bohrloch_abstand und bohrloch_durchmesser wurden automatisch erkannt und als Bedienelemente in den Customizer eingefügt. Falls der Customizer nichts anzeigt, dann hilft es, die Vorschau erneut berechnen zu lassen und anschließend ggf. auf das kleine Dreieck vor Parameters zu klicken. Man kann nun unterschiedliche Konfigurationen als sogenannte Presets speichern und laden. Diese Funktionalität funktioniert jedoch nur, wenn man die Geometriebeschreibung bereits als .scad-Datei gespeichert hat. Die Presets selbst werden in einer zweiten Datei gespeichert, die den gleichen Namen hat wie die .scad-Datei, jedoch auf .json endet.
Das Geometriemodell unserer Lochplatte ist inzwischen einigermaßen ausgereift. Was uns jetzt noch fehlt ist eine Möglichkeit, unsere Lochplatte komfortabel an mehreren Stellen einzusetzen ohne unsere Geometriebeschreibung kopieren zu müssen. Für diesen Zweck gibt es sogenannte Module in OpenSCAD:
module lochplatte( groesse, loch_dm, loch_abst) {
difference() {
cube( groesse );
randabstand = loch_abst + loch_dm/2;
x_lochdistanz = groesse.x - 2*randabstand;
y_lochdistanz = groesse.y - 2*randabstand;
x_werte = [randabstand : x_lochdistanz : groesse.x - randabstand];
y_werte = [randabstand : y_lochdistanz : groesse.y - randabstand];
// Bohrlöcher
for (x = x_werte, y = y_werte)
translate( [x, y, -1] )
color( "red" )
cylinder( d = loch_dm, h = groesse.z + 2);
}
}
lochplatte( [100,50,5], 6, 4 );
translate( [0,60,0] )
lochplatte( groesse = [50,50,5], loch_dm = 3, loch_abst = 2 );
translate( [60,60,0] )
lochplatte( [50,50,5], loch_dm = 5, loch_abst = 5 );Module werden in OpenSCAD durch das Schlüsselwort module eingeleitet. Es folgt der Name des Moduls (hier: lochplatte) und seine Parameterliste in runden Klammern. Wir müssen an dieser Stelle nicht angeben, welcher Art die Parameter sind. Die Art der Parameter wird von OpenSCAD automatisch anhand ihrer Verwendung ermittelt. So ist in unserem Beispiel der Parameter groesse ein dreidimensionaler Vektor, während loch_dm und loch_abst einfache Zahlen sind. Der Inhalt eines Moduls ist eine mit geschweiften Klammern eingefasste Geometriemenge - ganz so wie wir es bereits bei den Booleschen Operatoren kennengelernt haben.
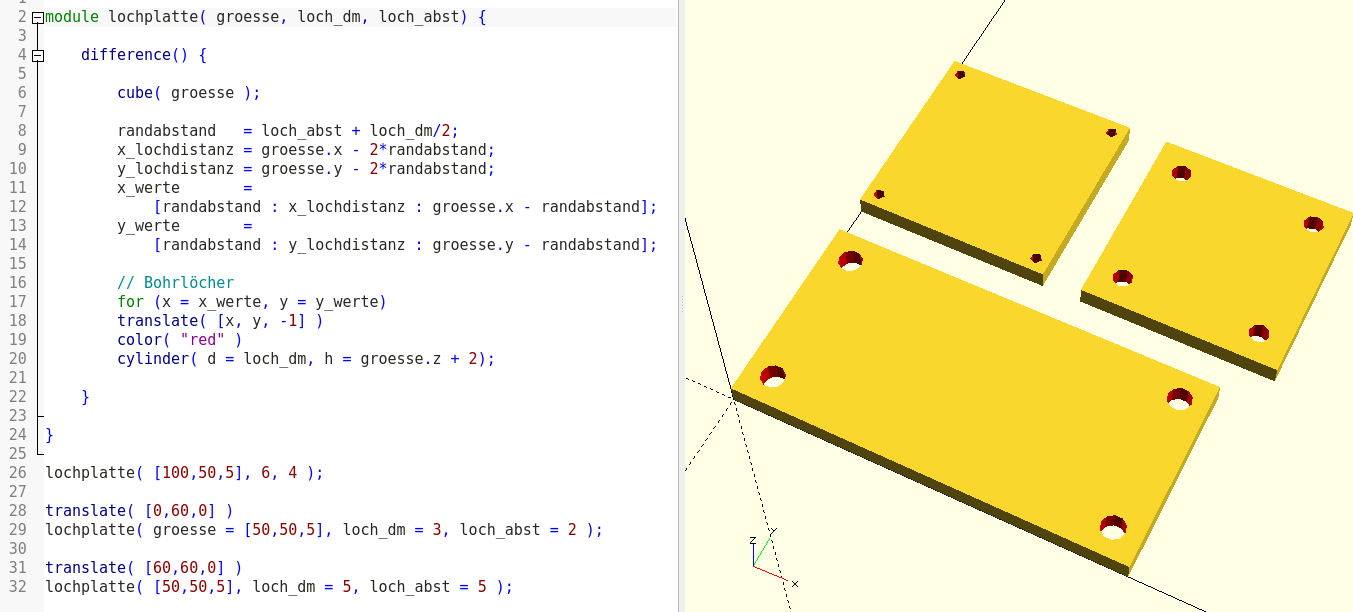
Hat man das Modul einmal definiert, kann man es wie eine der Grundformen (Kugel, Quader, etc.) verwenden. In unserem Beispiel haben wir drei Lochplatten erstellt, von denen wir zwei mittels Verschiebe-Transformationen (translate) arrangiert haben (Abbildung 2.).
Innerhalb des Moduls haben wir unsere ursprüngliche Geometriebeschreibung übernommen und lediglich die globalen Variablen durch die Variablen aus der Parameterliste des Moduls getauscht. Wir haben die letzte Variante aus dem vorhergehenden Abschnitt genommen, da wir diese nun nutzen können, um den Funktionsumfang unseres Moduls so zu erweitern, dass wir die Anzahl der Bohrungen parametrisieren können:
module lochplatte( groesse, loch_dm, loch_abst, anzahl = [2,2] ) {
difference() {
cube( groesse );
randabstand = loch_abst + loch_dm/2;
x_lochdistanz = (groesse.x - 2*randabstand) / (anzahl.x - 1);
y_lochdistanz = (groesse.y - 2*randabstand) / (anzahl.y - 1);
x_werte = [randabstand : x_lochdistanz : groesse.x - randabstand + 0.1];
y_werte = [randabstand : y_lochdistanz : groesse.y - randabstand + 0.1];
// Bohrlöcher
for (x = x_werte, y = y_werte)
translate( [x, y, -1] )
color( "red" )
cylinder( d = loch_dm, h = groesse.z + 2);
}
}
lochplatte( [100,50,5], 6, 4 );
translate( [0,60,0] )
lochplatte(
groesse = [50,50,5],
loch_dm = 3,
loch_abst = 2,
anzahl = [4,6]
);
translate( [60,60,0] )
lochplatte( [50,50,5], loch_dm = 5, loch_abst = 5, anzahl = [4,3] );Wir haben unserem Modul nun einen Parameter anzahl hinzugefügt und dem Parameter einen Standardwert gegeben (hier: [2,2], ein zweidimensionaler Vektor). Da wir für die For-Schleife zwei Spannen (x_werte und y_werte) verwendet haben, müssen wir nur die Schrittweiten x_lochdistanz und y_lochdistanz so anpassen, das die gewünschte Anzahl Löcher in X- und Y-Richtung erzeugt werden. Auch hier können uns Rundungsfehler in die Quere kommen. Daher müssen wir auch den Endwert der For-Schleifen leicht anpassen (+ 0.1). Da die tatsächlich in der Geometrie verwendeten Werte ausschließlich auf Basis der Schrittweiten ermittelt werden, erzeugen wir mit dieser Anpassung keine Ungenauigkeit in unserer Konstruktion.
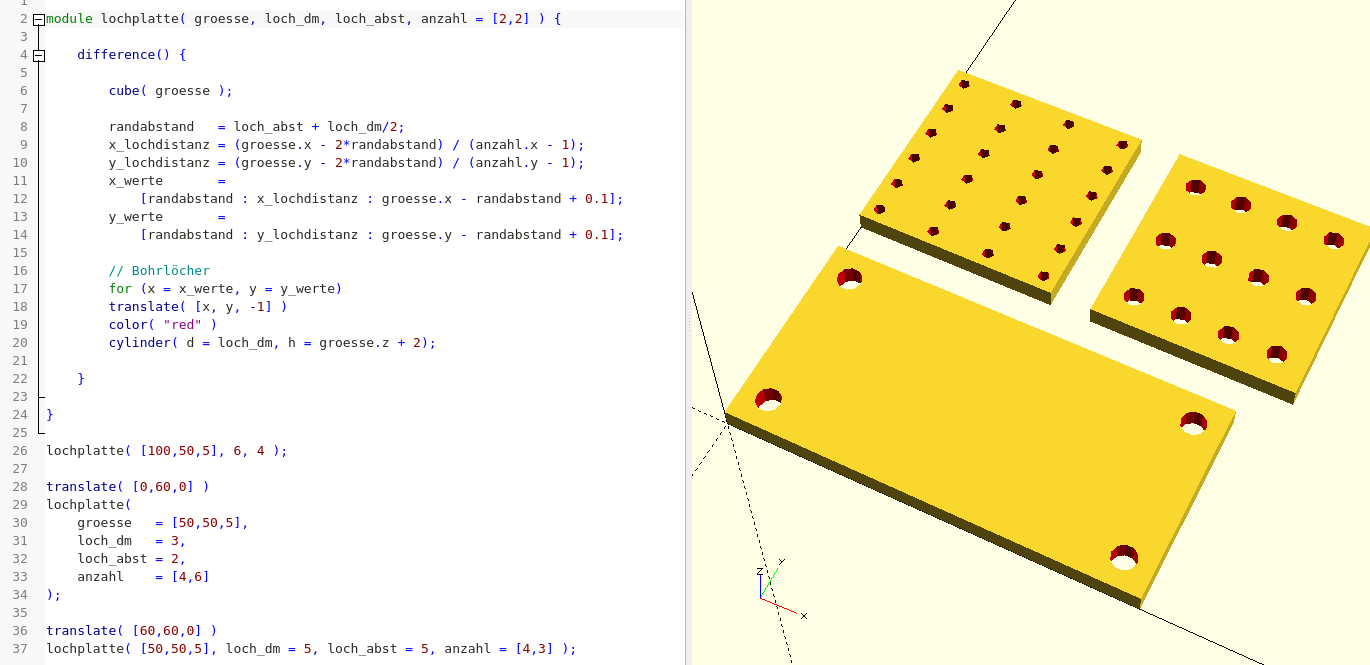
Da wir den neuen Parameter anzahl unseres Moduls mit einem Standardwert versehen haben, ist das Modul “abwärtskompatibel”. So hat sich die erste Verwendung unseres Moduls nicht verändert (Abbildung 2.).
Unser Modul hat noch ein paar Schönheitsfehler. Wenn der Parameter anzahl den Wert 1 enthält, dann enthält die Berechnung der zugehörigen Lochdistanz eine Division durch 0. Dies ist nicht gut und wir sollten uns unbedingt darum kümmern. Wie wäre es, wenn wir im Falle einer Anzahl von 1 das zugehörige Loch mittig platzieren? Um dies zu erreichen, brauchen wir eine Fallunterscheidung sowohl bei der Bestimmung der Lochdistanzen (x_lochdistanz und y_lochdistanz) als auch bei der Festlegung der Wertebereiche (x_werte und y_werte) der Schleifenvariablen:
module lochplatte( groesse, loch_dm, loch_abst, anzahl = [2,2] ) {
difference() {
cube( groesse );
randabstand = loch_abst + loch_dm/2;
x_lochdistanz = anzahl.x > 1 ? (groesse.x - 2*randabstand) / (anzahl.x - 1) : 0;
y_lochdistanz = anzahl.y > 1 ? (groesse.y - 2*randabstand) / (anzahl.y - 1) : 0;
x_werte = anzahl.x > 1 ?
[randabstand : x_lochdistanz : groesse.x - randabstand + 0.1] :
[groesse.x / 2];
y_werte = anzahl.y > 1 ?
[randabstand : y_lochdistanz : groesse.y - randabstand + 0.1] :
[groesse.y / 2];
// Bohrlöcher
for (x = x_werte, y = y_werte)
translate( [x, y, -1] )
color( "red" )
cylinder( d = loch_dm, h = groesse.z + 2);
}
}
lochplatte( [100,50,5], 6, 4 );
translate( [0,60,0] )
lochplatte(
groesse = [50,50,5],
loch_dm = 3,
loch_abst = 2,
anzahl = [1,1]
);
translate( [60,60,0] )
lochplatte( [50,50,5], loch_dm = 5, loch_abst = 5, anzahl = [2,1] );Die Fallunterscheidungen verwenden den Fragezeichenoperator, der ganz allgemein die Struktur a ? b : c hat. Der Teil a ist immer eine Ja- oder Nein-Frage (hier z.B.: “ist anzahl.x größer 1”). Wenn die Antwort ja ist, wird b als Wert genommen, wenn die Antwort nein ist, wird c als Wert genommen.
Wenn Sie etwas Programmiererfahrung haben, werden Sie vielleicht zuerst an einen if-Ausdruck gedacht haben, um die obige Fallunterscheidung vorzunehmen. Dies ist wieder so ein Fall, wo die “normale” Programmierintuition eher hinderlich ist. Wir können den Variablen in OpenSCAD ja nur einmal einen Wert geben! Der folgende Ausdruck würde in OpenSCAD daher nicht funktionieren:
x_lochdistanz = 0;
if (anzahl.x > 1) {
x_lochdistanz = (groesse.x - 2*randabstand) / (anzahl.x - 1);
}Dennoch gibt es auch das Schlüsselwort if in OpenSCAD. Man kann es verwenden, um ganze Teile der Geometriebeschreibung ein- oder auszuschließen. Wir können es in unserem Beispiel dazu nutzen, noch einen weiteren Schönheitsfehler in unserem Modul zu beseitigen. Im Moment würde eine Anzahl von 0 oder irgendeinem negativen Wert auch zu einem einzelnen Loch führen. Das scheint nicht zu passen. Wenn wir bei der Anzahl eine 0 angeben, dann wollen wir offenbar gar kein Loch:
module lochplatte( groesse, loch_dm, loch_abst, anzahl = [2,2] ) {
if (anzahl.x == 0 || anzahl.y == 0) {
cube( groesse );
} else {
difference() {
cube( groesse );
randabstand = loch_abst + loch_dm/2;
x_lochdistanz = anzahl.x > 1 ? (groesse.x - 2*randabstand) / (anzahl.x - 1) : 0;
y_lochdistanz = anzahl.y > 1 ? (groesse.y - 2*randabstand) / (anzahl.y - 1) : 0;
x_werte = anzahl.x > 1 ?
[randabstand : x_lochdistanz : groesse.x - randabstand + 0.1] :
[groesse.x / 2];
y_werte = anzahl.y > 1 ?
[randabstand : y_lochdistanz : groesse.y - randabstand + 0.1] :
[groesse.y / 2];
// Bohrlöcher
for (x = x_werte, y = y_werte)
translate( [x, y, -1] )
color( "red" )
cylinder( d = loch_dm, h = groesse.z + 2);
}
}
}
lochplatte( [100,50,5], 6, 4 );
translate( [0,60,0] )
lochplatte(
groesse = [50,50,5],
loch_dm = 3,
loch_abst = 2,
anzahl = [0,1]
);
translate( [60,60,0] )
lochplatte( [50,50,5], loch_dm = 5, loch_abst = 5, anzahl = [2,1] );Hier unterscheiden wir also gleich zu Beginn, ob wir eine Platte mit oder ohne Löcher modellieren wollen und verzweigen unsere Geometriebeschreibung entsprechend. Gleichheit wird mit dem doppelten Gleichheitszeichen (==) ausgedrückt. Die zwei senkrechten Striche (||) haben die Bedeutung eines logischen “oder” im Sinne von “es muss nur eine der beiden Fragen mit ja beantwortet werden”.
Nehmen wir an, wir möchten unsere Lochplatte in einem anderen Projekt wiederverwenden. Auch hier wäre es eine schlechte Idee, die Geometriebeschreibung einfach in das neue Projekt hineinzukopieren. OpenSCAD bietet zwei Befehle an, um andere .scad-Dateien in ein Projekt einzubinden:
include <lochplatte.scad>;Der include-Befehl lädt eine andere .scad-Datei (hier: lochplatte.scad) komplett in die aktuelle Geometriebeschreibung ein. Dies bedeutet, dass auch die drei Testplatten, die wir unterhalb unseres Moduls definiert haben, in der neuen Geometriebeschreibung auftauchen würden. Um dies zu vermeiden, gibt es in OpenSCAD anstelle des include-Befehls auch noch den Befehl use:
use <lochplatte.scad>;Verwendet man use anstelle von include werden nur die Module und Funktionen aus der anderen .scad-Datei übernommen. Die Datei, die man innerhalb der spitzen Klammern angibt, muss entweder im gleichen Verzeichnis liegen, wie die Datei der aktuellen Geometriebeschreibung, oder im Library-Folder (dt. Bibliotheksverzeichnis) von OpenSCAD. Über den Menüpunkt File -> Show Library Folder kann man sich das Bibliotheksverzeichnis anzeigen lassen und dort ggf. seine Geometriebibliotheken ablegen. Im Internet lassen sich bereits eine Reihe ganz ausgezeichneter Geometriebibliotheken für OpenSCAD finden. Das Bibliotheksverzeichnis ist der Ort, wo man diese hinkopieren muss, um sie zu verwenden.
Hat man eine Geometrie nicht als OpenSCAD-Geometriebeschreibung vorliegen, kann man eine ganze Reihe von Dateiformaten mit dem import-Schlüsselwort verwenden.
import("logo.svg");Die geladene Geometrie kann dann wie eine Grundform (Kugel, Quader, etc.) oder ein Modul verwendet werden (z.B. translate(...) import("logo.svg");). OpenSCAD unterstützt DXF und SVG als zweidimensionale Formate und STL, OFF, AMF und 3MF als dreidimensionale Formate.
Herzlichen Glückwunsch! Sie kennen jetzt alle wesentlichen Konzepte und Funktionsweisen von OpenSCAD. Alles weitere sind tatsächlich “nur” noch Details. In den nachfolgenden Beispielprojekten werden wir den Umgang mit diesen Konzepten üben und vertiefen und uns nach und nach die übrigen Details erarbeiten. Sie werden sehen, dass ihr Verständnis der Materie mit jedem Projekt schrittweise besser werden wird, so dass Sie bald eine klare Vorstellung davon haben, wie sie von einer Idee zu einer fertigen Geometriebeschreibung kommen.